1781
Toward Analytic Computation of Fiber-Radial Diffusional Kurtosis by Q-space Data Representation with Radial Basis Functions1Graduate School of Information Sciences, Hiroshima City University, Hiroshima, Japan, 2Hiroshima Heiwa Clinic, Hiroshima, Japan
Synopsis
To enhance the robustness of the fiber-radial diffusional kurtosis computation, the signal decay in the Q-space can be averaged among the fiber-radial orientations. By using the radial basis functions with Gaussian basis, it is shown that the fiber-radial signal decay can be represented in a pseudo-analytic form with the Bessel function. By using in-vivo diffusion MRI data, the computation results were presented in comparison with those by diffusion kurtosis tensor of 4th order to prove the effectiveness of the proposed method.
INTRODUCTION
Diffusional kurtosis is known as the non-Gaussianity of the water diffusion probability distribution function, and also as the useful tools to evaluate the normal and pathological tissues mainly in the neurological area. The technique of the Diffusional Kurtosis Imaging (DKI) [1] provides us of the diffusional kurtosis values by fitting a series of measured signal values with multiple b-values and directions of motion sensitizing gradient to the DKI signal model. When the diffusional kurtosis is evaluated in the white matter with certain diffusion anisotropy due to the fibrous structures, diffusional kurtosis values in the two orientations are often employed, which are fiber-axial kurtosis and fiber-radial kurtosis. Particularly, the latter value reflects the restriction state of the water diffusion influenced by the local microstructural parameters such as the diameter and density of the axon. The diffusional kurtosis values of fiber-axial and fiber-radial orientations are basically obtained by using the diffusional kurtosis tensor of the 4th order [1]. However, it is hard to estimate the oriented kurtosis values robustly due to the sensitivity to the noise. In this short abstract, we describe a method for estimation of the fiber-radial kurtosis values with enhanced robustnesss and in a pseudo-analytic manner with the Q-space data representation by radial basis functions (RBF) [2]. Experimental results by comparison with diffusional kurtosis tensor method are also presented to prove its potential effectiveness.
METHODS
(1) Fiber-Radial Signal Decay Averaging
To obtain the fiber-radial kurtosis value, we first reconstruct a smooth series of signal decays by line integral in Q-space (Fig.1). That is, we average the signal decay values on the circle with radius $$$q$$$ perpendicular to fiber direction in Q-space, similarly to the Funk-Radon transform of QBI [3]. If the fiber orientation is given as $$${{\bf{v}}_f}$$$, we can define a unique and smoothed signal decay $$${E_{\bot {\bf{v}}_f}}$$$ for a q-value $$${q}$$$ as follows.
$$E_{\bot {\bf{v}}_f}(q) =\frac{1}{{2\pi q}} {\oint_{\bf{q}\bot{{\bf{v}}_\it{f}},\parallel\bf q\parallel=\it {q} } E(\bf q)}$$
$$$E({\bf q})$$$ is the signal decay function in Q-space, which is interpolated with measured signal decays by using radial basis functions in our study.
(2) RBF Representation of Signal Decay
When a Q-space data set is given as a series of pairs of q-vector $$${\bf{q}}_\it{i}$$$ and measured signal decay value $$$E_i$$$ at $$${\bf{q}}_\it{i}$$$ $$$(i=0,…,N)$$$, we can obtain signal decay value at arbitrary location $$$\bf{q}$$$ by using radial basis functions [2] as below.
$$E({\bf q}) =\sum_{i=0}^N w_{i}\cdot \phi(\parallel\bf{q}-\bf{q}_{\it i}\parallel)$$
Note that $$${\bf q}_0={\bf{O}}, E_0=1$$$ and $$$N$$$ is the number of the measured signals duplicated by a point-symmetry assumption $$$E(-{\bf q})=E({\bf q})$$$. The weights $$$w_i$$$ are simply estimated by the matrix methods of linear least squares, and $$$\phi(r)$$$ is the basis function.
(3) Gaussian Basis and Fiber-Radial Signal Decay with the Bessel Functions
When we use the Gaussian basis $$$\phi(r)=e^{-(\epsilon \cdot r)^2}$$$, we get $$$E_{\bot {\bf v}_{\it f} }(q)$$$ in a pseudo-anlaytic form as follows.
$$E_{\bot {\bf{v}_\it{f}}}(q) =\frac{1}{{2\pi q}} {\oint_{\bf{q}\bot {\bf{v}_\it{f}},\parallel\bf{q}\parallel=\it {q} } \sum_{i=0}^N w_{i}\cdot e^{-(\epsilon\cdot \parallel\bf{q}-\bf{q_{\it i}}\parallel)^{2}}}\\=\frac{1}{{2\pi q}} \sum_{i=0}^N w_{i}\cdot e^{-\epsilon^2(q^2+{\parallel\bf{q_{\it i}}\parallel}^2)}\int_{0}^{2\pi} e^{2\epsilon^2\sqrt{\parallel\bf{q_{\it i}}\parallel^2-({\bf{v}_\it{f}}\cdot \bf{q_{\it i}})^2}\cos\theta}d\theta\\=\frac{1}{q} \sum_{i=0}^N w_{i}\cdot e^{-\epsilon^2(q^2+{\parallel\bf{q_{\it i}}\parallel}^2)}\cdot I_0(2\epsilon^2 \small {\sqrt{\parallel\bf{q_{\it i}}\parallel^2-({\bf{v}_\it{f}}\cdot \bf{q_{\it i}})^2}})$$
$$$I_0(\cdot)$$$ is the 0-th order modified Bessel function of the first kind, that is, $$$I_0(z)=\sum_{k=0}^{\infty}\frac{(\frac{1}{4}z^2)^k}{(k!)^2}$$$. Finally, we can obtain the kurtosis value with series of signal decays $$$E_{\bot \bf{v}_\it{f}}(q)$$$ by using the closed-form expression [4] with conversion of q-values to b-values. For fiber orientation estimation, a diffusion tenor model of the 2nd order is employed in this study.
RESULTS AND DISCUSSION
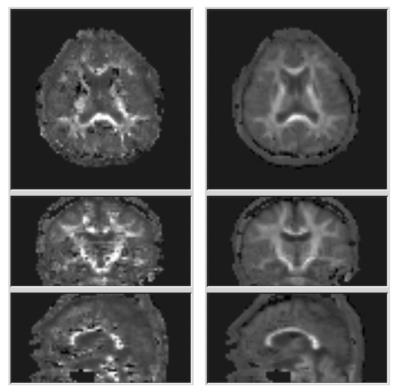
We used an in-vivo DWI data set of a healthy volunteer in an 80x80x40 matrix size, obtained with 32 directions of motion sensitizing gradient, and 5 b-values; 500 to 2500 with 500 step ($$$s/mm^2$$$). We compared the fiber-radial kurtosis images visually between diffusion kurtosis tensor method and our method as shown in Fig.2. Apparently, the black artifact due to the underestimation of kurtosis values yielded by noise in original DWI are reduced. Also, thanks to the pseudo-analytic form of the fiber-radial signal decay value, no high computational cost is required. The computation time was a few minutes with a standard PC workstation. In this study, we used Gaussian basis function and therefore computed the Bessel function values of the infinite series in a numerical manner with a limited extent of series. However, another basis function might allow us to compute the signal decay values in a fully-analytic and closed form.CONCLUSION
We proposed a method for robustness enhancement in computation of the fiber-radial diffusional kurtosis values, by signal decay averaging in fiber-radial orientations with Q-space data representation with radial basis functions. The experimental results by in-vivo data proved its potential effectiveness.Acknowledgements
Authors are grateful to Dr. Shigeki Aoki and Dr. Masaaki Hori for providing us of the in-vivo data set employed in this abstract.References
1. Jensen JH, Helpern JA, Ramani A, et al. Diffusional kurtosis imaging: the quantification of non-Gaussian water diffusion by means of magnetic resonance imaging. Magn Reson Med 2005; 53: 1432–1440.
2. Buhmann MD. Radial Basis Functions: Theory and Implementations, Cambridge University Press, Cambridge, UK, 2003.
3. Tuch DS. Q-ball imaging. Magn Reson Med. 2004 Dec;52(6):1358-72.
4. Masutani Y and Aoki S. Fast and robust estimation of diffusional kurtosis imaging (DKI) parameters by general closed-form expressions and their extensions. Magn Reson Med Sci 2014;13:97–115.