Synopsis

This study investigates the sensitivity of the Stimulated-Echo Acquisition Mode (STEAM) diffusion-weighted signal to permeability quantified with water exchange time $$$\tau_{ex}$$$. In order to do this, Monte Carlo simulations were generated for a range of histologically-plausible $$$\tau_{ex}$$$ and practical scanner acquisition parameters. The results suggest that on the standard clinical scanner (G=70mT/m), STEAM estimates short exchange times (<0.9s), which are characteristic in tissue with myelin damage, while tissue with longer exchange times (>1.5s) is practically indistinguishable from impermeable tissue. The Connectome scanner (G=300mT/m) estimates a much wider range, however needs careful optimisation since the resolution limit is highly dependent on the sequence parameters and SNR’s.

Purpose

This work aims to study the feasibility of Stimulated-Echo Acquisition Mode (STEAM) diffusion-weighted MRI to estimate water exchange time $$$\tau_{ex}$$$ in brain white matter (WM), a parameter inversely related to the permeability of brain tissue. The estimation of $$$\tau_{ex}$$$ is an important biomarker for WM pathologies such as Multiple Sclerosis (MS) since the myelin damage characteristic of these pathologies is hypothesised to lead to an increase in permeability and thus a decrease in the $$$\tau_{ex}$$$. STEAM offers benefits over Pulsed-Gradient Spin-Echo (PGSE)⁶ as it allows for longer diffusion times and it is, therefore, more suitable for measuring $$$\tau_{ex}$$$.

Here, we use Monte Carlo simulations to investigate the sensitivity of STEAM sequences to $$$\tau_{ex}$$$ over a range of histologically plausible exchange times and WM substrates. We explore combinations of STEAM acquisition parameters covering clinically plausible settings. Finally, we calculate the water exchange resolution limit defined as the largest identifiable $$$\tau_{ex}$$$ above which one cannot distinguish from identical impermeable substrates (where $$$\tau_{ex}=\infty$$$).

Methods

Monte Carlo simulations of signals from WM substrates are used to analyse the sensitivity to water exchange time of STEAM sequences. Brain WM tissue was modelled using substrates of gamma-distributed, permeable, non-abutting parallel cylinders generated using Camino¹. Signals are simulated using 100,000 spins and 2000 time steps¹ with diffusivity D=1.7×10⁻⁹m²s⁻¹, f=[0.4,0.7] as standard values in WM². Two substrates with gamma distributions of histologically plausible cylinder radii³ were modelled to mimic small and large axons in brain WM (volume-weighted radius index of 0.3µm and 1µm respectively². The signals from the two substrates were simulated for exchange times $$$\tau_{ex}$$$ between 0s and 2.5s representing a physiologically plausible range^4,5.

We used STEAM sequences with the following parameters: gradient duration $$$\delta \in$$$[10,20,30]ms, diffusion time $$$\Delta\in$$$[150,300,480]ms and gradient strength G=[70,300] mT/m corresponding to standard clinical scanner and Connectome scanner respectively. The diffusion gradients were perpendicular to the cylinders in order to maximise sensitivity to the water exchange time.

Results

Figure 1 shows the signal dependence on the exchange time for volume fraction of 0.4 (top row) and 0.7 (bottom row) for small (left) and large (right) axon diameters. The plots show that the signal changes the most for exchange times that are smaller than 1s, however after that the signal converges. This trend is present for all substrates.

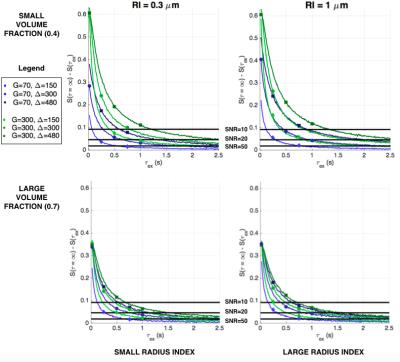
Figure 2 shows the difference between the signals in Figure 1 and the signal for impermeable substrates. This difference illustrates whether the exchange time effect can be detected in the signal, i.e. whether it can be distinguished from signals coming from impermeable cylinders. As the effect depends on the amount of noise present, the horizontal lines mark detection levels for SNRs of 10, 20 and 50 for small (column 1) and large (column 2) volume-weighted axon radii indices. The plots show that the effect of the exchange time has a wider detectable range for larger volume fraction. Furthermore, while changes in signal for very short exchange times result in a distinguishable change in signal, for large $$$\tau_{ex}$$$ the change in signal is below the noise threshold for all substrates and sequence parameters.

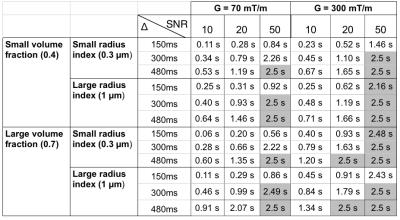
Table 1 quantitatively shows the resolution limit of the detectable range of exchange times for different sequence parameters and SNR levels when $$$\delta$$$=10ms. The resolution limit represents the largest distinguishable $$$\tau_{ex}$$$ above which one cannot distinguish from identical impermeable substrates (where $$$\tau_{ex}$$$=∞), i.e. larger the resolution limit larger the range of permeabilities that can be detected. The table shows that the largest resolution limit is achieved for the longest diffusion time and largest gradient strength.

Discussion and Conclusions

The results show that on the standard clinical scanner (G=70mT/m), STEAM sequence can estimate short exchange times (<0.9s), which are characteristic in tissue with myelin damage^6. Substrates with longer exchange times (>1.5s), which are characteristic in healthy WM tissue⁴ are practically indistinguishable from impermeable substrates. The Connectome scanner (G=300mT/m) estimates a much wider range, however needs careful optimisation since the resolution limit is highly dependent on the sequence parameters and SNR’s. We also showed that the longest diffusion time $$$\Delta$$$ maximises the resolution limit. We note that here we considered only $$$\delta$$$=10ms and $$$\Delta$$$ up to 480ms. Further increasing $$$\Delta$$$ would increase the resolution limit, however it would also decrease the SNR due to additional T1 decay. Increasing $$$\delta$$$ would also increase the resolution limit, especially for weak gradient strengths. Nevertheless, it would drastically impact SNR due to an increase in echo time and T2 decay.

Acknowledgements

References

[1] Hall MG and Alexander DC. Convergence and parameter choice for Monte-Carlo simulations of diffusion MRI. IEEE T Med Imaging 2009; 28(9): 1354-1364.

[2] Alexander, Daniel C., et al. Orientationally invariant indices of axon diameter and density from diffusion MRI. Neuroimage 52.4 (2010): 1374-1389.

[3] Aboitiz, Francisco, et al. Fiber composition of the human corpus callosum. Brain research 598.1 (1992): 143-153.

[4] Nilsson, Markus, et al. Noninvasive mapping of water diffusional exchange in the human brain using filter-exchange imaging. Magnetic resonance in medicine 69.6 (2013): 1572-1580.

[5] Quirk, James D., et al. Equilibrium water exchange between the intra-and extracellular spaces of mammalian brain. Magnetic resonance in medicine 50.3 (2003): 493-499.

[6] Nedjati-Gilani, Gemma L., et al. Machine learning based compartment models with permeability for white matter microstructure imaging. International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer International Publishing, 2014.