1761
Multi-Spherical Diffusion MRI: An in-vivo Test-Retest Study of Time-Dependent q-space Indices1Universite Cote d'Azur, Inria, France, Sophia Antipolis, France, 2CENIR, Institut du Cerveau et de la Moelle epineere, Paris, France
Synopsis
Effective representation of the diffusion signal's dependence on diffusion time is a sought-after challenge in diffusion MRI (dMRI). As a solution, we recently proposed Multi-Spherical Diffusion MRI (MS-dMRI) to represent the dMRI signal in this four-dimensional space - varying over gradient strength, direction and diffusion time. Our representation allows for the estimation of time-dependent q-space features, providing unique insights on the tissue microstructure. In the study, we assess test-retest reproducibility of these indices in three C57Bl6 wild-type mice. We find that due to our effective regularization methodology during signal fitting, these time-dependent features can be estimated reliably without overfitting the data.
Introduction
Studying the diffusion time-dependence of the diffusion signal is currently a hot topic in the diffusion MRI community. To this end, we recently proposed the Multi-Spherical Diffusion MRI (MS-dMRI) functional basis approach [1, 2] to represent the dMRI signal in this four-dimensional space - varying over gradient strength, direction and diffusion time - that we call the multi-spherical space. MS-dMRI allows for the estimation of time-dependent q-space features, providing unique insights on the tissue microstructure [3]. To assess the reliability of their estimation, we quantify both the fitting error of the measured signal and the reproducibility of these features in a test-retest study.Methods
MS-dMRI represents the diffusion signal attenuation $$$E(\textbf{q},\tau)=S(\textbf{q},\tau)/S_0$$$ at diffusion encoding position $$$\textbf{q}$$$ and diffusion time $$$\tau$$$. It uses an orthogonal basis that allows efficient representation of any multi-spherical diffusion signal with few parameters $$$\textbf{c}$$$, using effective regularization approaches imposing signal smoothness and sparsity. We follow Callaghan et al.'s description of time-dependent diffusion in pores and assume an infinitely short gradient pulse $$$\delta\rightarrow0$$$ and separability in the dependence of the dMRI signal to $$$\textbf{q}$$$ and $$$\tau$$$ [4]. We represent the fitted signal attenuation using the cross-product between the spatial Fourier basis $$$\Phi_i(\textbf{q})$$$ [5] and temporal basis $$$T_k(\tau)$$$ [2] such that we fit $$$\hat{E}(\textbf{q},\tau;\textbf{c}) = \sum_i^{N_\textbf{q}}\sum_k^{N_\tau} \textbf{c}_{ik}\,\Phi_i(\textbf{q})\,T_k(\tau)$$$ with basis coefficients $$$\textbf{c}$$$ and $$$N_\textbf{q}$$$ and $$$N_{\tau}$$$ the number of spatial or temporal basis functions, respectively. The voxel-wise optimization is as follows:
$$ \textrm{argmin}_{\textbf{c}} \overbrace{\iint\left[E(\textbf{q},\tau) - \hat{E}(\textbf{q}, \tau ; \textbf{c})\right]^2d\textbf{q}d\tau}^{\textrm{Data Fidelity}}+ \overbrace{\iint\left[\nabla^2 \hat{E}(\textbf{q}, \tau; \textbf{c})\right]^2d\textbf{q}d\tau}^{\textrm{Smoothness}} + \overbrace{\|\textbf{c}\|_1}^{\textrm{Sparsity}},\textrm{ subject to}\overbrace{\hat{E}(0, \tau;\textbf{c})=1}^{\textrm{Attenuation Boundary Condition}}$$
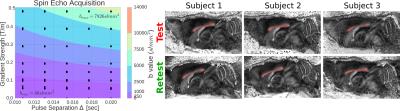
Once the coefficients $$$\textbf{c}$$$ are known, we can directly estimate features of the multi-spherical diffusion propagator $$$\hat{P}(\textbf{R},\tau;\textbf{c})$$$ through our spatial basis' Fourier properties [5]. We illustrate this by computing the time-dependent indices for the Mean Squared Displacement (MSD) [6]; and Return-To-Origin, Return-To-Axis and Return-To-Plane Probability (RTOP, RTAP and RTPP) [5], whose values are inversely related to the mean, perpendicular and parallel diffusivity, respectively. We apply our method in-vivo to three C57Bl6 wild-type mice. For each mouse we acquire test-retest spin-echo multi-spherical images in an 11.7 Tesla Bruker scanner. We show our scheme on the left of Figure 1. We acquire 35 different ``shells'' with one b0 each and a total of 480 DWIs using $$$\delta=5ms$$$. We measure five equispaced "$$$\tau$$$-shells" $$$\Delta=\{10.8, 13.1, 15.4, 17.7, 20 \}$$$ms and seven approximately equispaced "gradient shells" between $$$\{50-490\}$$$mT/m. The voxels are of size $$$100\times 100\times 500\,\mu \textrm{m}$$$. We corrected each dataset from eddy currents and motion artifacts using FSL's eddy_correct, and drew a region of interest in the middle slice of the corpus callosum, taking voxels with Fractional Anisotropy $$$>0.45$$$. We show a sagittal slice with the ROIs on the right of Figure 1.
Results
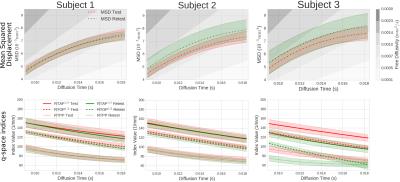
To ensure that we are not overfitting the data we analyze the fitting error of our technique on a random subset of the data and predict the missing values. For every subject, we show the mean squared error (MSE) of the regularized model fitting in Figure 2. It can be seen that the MSE is similar for all datasets except for the Test Subject 3, which is almost twice as high. We then estimate and illustrate the time-dependent indices: MSD, RTOP, RTAP and RTPP in Figure 3. As expected, the MSD increases and RTOP, RTAP, and RTPP decrease over diffusion time as particles can travel further as time increases. Subject 1 shows that, for all indices, the mean retest indices fall within 0.2 standard deviations of the test indices with similar dispersion. Subject 2 shows similar overlap for the q-space indices, but the retest MSD is slightly off. Subject 3 does not show the same consistency, which corresponds to the higher fitting error found in Figure 2.Discussion
We assessed the reproducibility of time-dependent, microstructurally-relevant q-space indices using our MS-dMRI approach. In two out of the three mice we found these indices to be well reproducible within a region of interest in the corpus callosum (see in Figure 3). The results of subject 3 appear less consistent, which corresponds to the higher fitting error of Test Subject 3 in Figure 2. DTI analysis in this data also reveals relatively lower FA values in the corpus callosum compared to the other datasets. Therefore, this inconsistency appears to be a particularity of the data itself and not our method.Conclusion
We showed that we can robustly and consistently estimate time-dependent q-space indices using MS-dMRI in in-vivo diffusion spin echo acquisitions of C57Bl6 wild-type mice. This result underlines the feasibility of using MS-dMRI in the analysis of time-dependent features of the diffusion signal.Acknowledgements
This work has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program(ERC Advanced Grant agreement No 694665 : CoBCoM) and MAXIMS grant funded by ICM's The Big Brain Theory Program and ANR-10-IAIHU-06.References
[1] Fick, Rutger, et al. "Multi-Spherical Diffusion MRI: Exploring Diffusion Time Using Signal Sparsity." MICCAI 2016 Workshop on Computational Diffusion MRI (CDMRI'16). 2016.
[2] Fick, Rutger, et al. "A unifying framework for spatial and temporal diffusion in diffusion MRI." International Conference on Information Processing in Medical Imaging. Springer International Publishing, 2015.
[3] Ozarslan, Evren, et al. "Observation of anomalous diffusion in excised tissue by characterizing the diffusion-time dependence of the MR signal." Journal of Magnetic Resonance 183.2 (2006): 315-323.
[4] Callaghan, Paul T. "Pulsed-gradient spin-echo NMR for planar, cylindrical, and spherical pores under conditions of wall relaxation." Journal of Magnetic Resonance, Series A 113.1 (1995): 53-59.
[5] Ozarslan, Evren, et al. "Mean apparent propagator (MAP) MRI: a novel diffusion imaging method for mapping tissue microstructure." NeuroImage 78 (2013): 16-32.
[6] Fick, Rutger HJ, et al. "MAPL: Tissue microstructure estimation using Laplacian-regularized MAP-MRI and its application to HCP data." NeuroImage 134 (2016): 365-385.
Figures