1743

Inferring cell morphology in the heart with a compartment model of diffusion MRI
Darryl McClymont1, Irvin Teh1, Hannah Whittington1, Craig Lygate1, and Jürgen Schneider1

1Cardiovascular Medicine, University of Oxford, Oxford, United Kingdom

Synopsis

We propose a three-compartment model to perform cytometry in cardiac diffusion MRI. Our approach adapts the VERDICT model to account for the anisotropic geometry of cardiomyocytes. The model was fit to data from ex-vivo mouse heart imaged with multiple diffusion times, diffusion directions, and q-shells. The model yields realistic volume fractions (intracellular/extracellular/vascular = 68/16/16%) and cell radii (7-9.5 μm). The parameters derived could aid quantitative characterisation of cardiomyopathies including hypertrophy and fibrosis.

Purpose

Diffusion-weighted imaging is sensitive to microstructural features orders of magnitude below typical MR resolution. Conventional diffusion tensor imaging assumes a single compartment and unrestricted diffusion. In contrast, models comprising hindered and restricted diffusion compartments allow the identification of diffusion from multiple environments within a voxel.

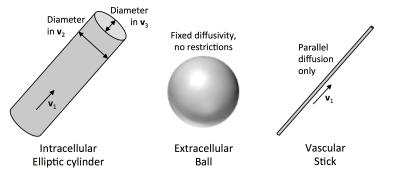
One such model is the VERDICT (Vascular, Extracellular and Restricted Diffusion for Cytometry in Tumours) model1. VERDICT has three compartments, namely a restricted sphere representing intracellular water, an isotropic tensor representing extracellular water, and a stick representing water in the capillary network. As myocardial cells are highly anisotropic, we instead model the intracellular component using an elliptic cylinder, which allows for differences in cell width and depth2. Our model provides estimates of microstructural parameters, including intracellular, extracellular and vascular volume fractions and cell size, which could potentially serve as quantitative biomarkers for cardiomyopathies including hypertrophy and fibrosis.

Methods

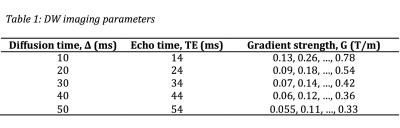
One ex-vivo mouse heart was scanned using a fast spin echo sequence on a 9.4T preclinical MR scanner. Images were acquired with six gradient strengths and five diffusion times (Δ) as presented in Table 1, and ten diffusion-encoding directions. One non-DW image was also acquired for each diffusion time, bringing the total number of images to 305. The remaining imaging parameters are as follows: resolution = 187.5 μm isotropic, field of view = 9×9×5 mm, echo train length = 8, echo spacing = 3.4 ms, diffusion duration δ = 2.5 ms, maximum b-value = 2500 s/mm2.

We utilise the three compartment model presented in Figure 1, consisting of (i) an elliptic cylinder representing the intracellular component; (ii) an isotropic tensor (ball) representing the extracellular space; and (iii) an infinitely thin cylinder (stick) representing the vascular component of the signal. The fitting parameters were estimated using the Levenburg-Marquardt optimiser in Camino3.

Results

Figure 2 presents the fitting performance of the model compared to the diffusion tensor model. Overall, the proposed model had a root mean square error (RMSE) of 2.7±0.7%, whereas the DTI model had a RMSE of 3.7±1.1% relative to the non-DW signal intensity.

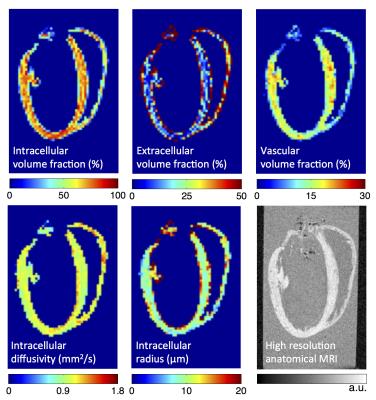
Figure 3 presents maps of the proposed model parameters. The right ventricle typically yielded higher extracellular volume fractions, most likely due to increased contributions from the gel and buffer from partial voluming. The model yielded radii in the secondary eigenvector direction that were much larger (>30 μm) than typical cells, indicating intracellular diffusion resembling a thin plane, rather than a cylinder.

Discussion

Our results are in agreement with the estimates of mouse myocardial extracellular volume fraction 20-32% by Neilan et al.4, depending on age and left ventricular mass. Our estimate of the vascular component is also in agreement with the estimate of the intracapillary blood volume of 12.9% using an extravascular contrast agent5, and 11.1% using the intravoxel incoherent motion method6.

The model assumes parallel alignment of cells and blood vessels, given that capillaries in the heart are known generally to run parallel with the cardiomyocytes7. One limitation of the presented model is that it does not incorporate cell dispersion. At the resolution employed in this study, each voxel may contain a range of helix angles of up to 30°. The inclusion of cell dispersion into the model may help to yield more physically plausible radii in the secondary eigenvector. Furthermore, the assumption that the vascular component has zero radius may have had a large impact on the model parameters. The use of a cylinder with a small radius, or distribution of radii8, may improve the model.

This study employed different echo times for each diffusion time, which allows for the possibility of errors to be introduced by different compartments having different T2 values. To address this, we applied echo time correction using the approach described by McClymont et al.9 using a bi-exponential T2-decay model. The fitting performance (not shown here) indicates only minor differences compared to fitting without echo time correction. This concurs with the findings of Kim et al.10, who investigated the effects of echo time when fitting a cylinder-ball model.

Conclusion

In this work we propose a three-compartment model of diffusion in healthy mouse myocardial tissue, assigning simple geometries to the intracellular, extracellular, and vascular compartments. While this model is a gross oversimplification of the true microstructure, the estimated parameters are in agreement with prior literature. Nevertheless, the measurement of volume fractions and cell sizes with high-resolution imaging is required for full model validation. The biophysical parameters derived from this model, including volume fractions and cell diameter, have the potential to act as valuable quantitative biomarkers for the characterisation of hypertrophy and fibrosis.

Acknowledgements

This work was supported by the British Heart Foundation (BHF) [grant numbers PG/13/33/30210, RG/13/8/30266, FS/11/50/29038, FS/12/17/29532 and NH/13/30238], the Engineering and Physical Sciences Research Council [grant number EP/J013250/1], and the BHF Centre for Research Excellence [grant number RE/13/1/30181. The authors acknowledge a Wellcome Trust Core Award [grant number 090532/Z/09/Z]; and the European Research Council Advanced Grant [CardioNECT].

References

1. Panagiotaki E, Walker-Samuel S, Siow B, Johnson SP, Rajkumar V, Pedley RB, Lythgoe MF, Alexander DC. Noninvasive quantification of solid tumor microstructure using VERDICT MRI. Cancer Res 2014;74(7):1902-12.

2. Satoh H, Delbridge LM, Blatter LA, Bers DM. Surface:volume relationship in cardiac myocytes studied with confocal microscopy and membrane capacitance measurements: species-dependence and developmental effects. Biophys J 1996;70(3):1494-504.

3. Cook P, Bai Y, Nedjati-Gilani S, Seunarine K, Hall M, Parker G, Alexander D. Camino: open-source diffusion-MRI reconstruction and processing. 2006. Seattle WA, USA.

4. Neilan TG, Coelho-Filho OR, Shah RV, Abbasi SA, Heydari B, Watanabe E, Chen Y, Mandry D, Pierre-Mongeon F, Blankstein R and others. Myocardial extracellular volume fraction from T1 measurements in healthy volunteers and mice: relationship to aging and cardiac dimensions. JACC Cardiovasc Imaging 2013;6(6):672-83.

5. Wacker CM, Wiesmann F, Bock M, Jakob P, Sandstede JJ, Lehning A, Ertl G, Schad LR, Haase A, Bauer WR. Determination of regional blood volume and intra-extracapillary water exchange in human myocardium using Feruglose: First clinical results in patients with coronary artery disease. Magn Reson Med 2002;47(5):1013-6.

6. Callot V, Bennett E, Decking UK, Balaban RS, Wen H. In vivo study of microcirculation in canine myocardium using the IVIM method. Magn Reson Med 2003;50(3):531-40.

7. Poole DC, Batra S, Mathieu-Costello O, Rakusan K. Capillary geometrical changes with fiber shortening in rat myocardium. Circ Res 1992;70(4):697-706.

8. Panagiotaki E, Schneider T, Siow B, Hall MG, Lythgoe MF, Alexander DC. Compartment models of the diffusion MR signal in brain white matter: a taxonomy and comparison. Neuroimage 2012;59(3):2241-54.

9. McClymont D, Teh I, Whittington HJ, Grau V, Schneider JE. Prospective acceleration of diffusion tensor imaging with compressed sensing using adaptive dictionaries. Magn Reson Med 2016;76(1):248-58.

10. Kim S, Chi-Fishman G, Barnett AS, Pierpaoli C. Dependence on diffusion time of apparent diffusion tensor of ex vivo calf tongue and heart. Magn Reson Med 2005;54(6):1387-96.

Figures

Table 1: DW imaging parameters

Figure 1: Diagram of the compartmental model. In total, the model has nine independent parameters: three to describe the orientation of the cylinder and stick, three to describe the diffusivity and radii of the cylinder, two to describe the volume fractions of the compartments, and one to describe the non-diffusion weighted signal S0. The compartments were aligned to the eigenvectors v1,2,3 of the diffusion tensor derived from the =10ms images. The diffusivity of the ball and stick was equal to that of the buffer (mm2/s).

Figure 2: Fitting performance of the diffusion tensor model and the proposed model in a representative voxel in the mesocardium. The presented data points represent the closest acquired direction to the three eigenvectors – the angular differences are 14, 17, and 24 degrees respectively. The diffusion tensor model provides a reasonable fit to the data in the primary eigenvector, but fails to capture the non-Gaussian behaviour in the secondary and tertiary eigenvectors. The proposed model yields a better fit to the data, particularly in the tertiary eigenvector direction.

Figure 3: Maps of the proposed model parameters. Partial voluming at the epicardium and endocardium with the isotropic gel and buffer results in higher estimates of extracellular volume fraction. Excluding regions exhibiting partial voluming, the intracellular volume fraction is 68±10%, the extracellular volume fraction is 16±11%, and the vascular volume fraction is 16±3%. The diffusivity within the intracellular component was 1.0±0.1×10-3 mm2/s, and the radius in v3 ranged between 7 and 10μm. For reference, a higher resolution anatomical image is also presented.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
1743