Synopsis

The anomalous diffusion behavior of biological tissue has been investigated by several studies using non-Gaussian diffusion models. Among these, the fractional motion (FM) model has attracted an intense interest by the biophysics community and was recently been introduced to the MR community. The current diffusion signal formulism based on the FM model is limited to a simple Stejskal-Tanner gradient despite the widespread use of the eddy-current-resistant gradient waveform with the twice-refocused spin echo (TRSE) technique. In this study, we theoretically derive a formulism based on the FM diffusion model to characterize anomalous diffusion using a TRSE sequence, and experimentally validate it on healthy human brain in vivo.

Introduction

Theory

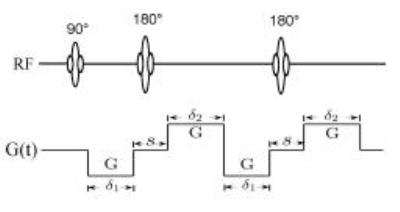
The FM diffusion model is based on Langevin motion, which is a unified statistical form for motions with power-law Fourier and kernel functions⁹. Considering correlated consecutive diffusion increments as a result of power law, the signal attenuation due to diffusion takes the following form: $$S/S_0=exp(-D_{φ,ψ} \int_{0}^{T_0}|F(t)|^φ dt), [1] $$ $$F(t)=\int_{t}^{T_0} γG(τ) (τ-t)^{H-1/φ}dτ, [2]$$ where D_φ,ψ is an anomalous diffusion coefficient (mm²/s), and φ and ψ are the parameters governing the variance and correlation properties of the increments of diffusion. The term, $$$(τ-t)^{H-1/φ}$$$, is a power law memory kernel^7,9 with the Hurst exponent $$$H=ψ/φ$$$¹⁰. For the TRSE implementation that balances the concomitant gradient fields¹¹, the gradient waveform (Fig. 1) consists of two bipolar gradients of length $$$δ_1$$$ and $$$δ_2$$$and, an inter-gradient separation, s. The diffusion-weighted (DW) signal attenuation for a TRSE sequence can be computed by obtaining F(t) in Eq.[2] for the gradient waveform, leading to the following signal equation: $$S/S_0=exp(-η^{''}D_{φ,ψ}(γG)^{φ}Δ_1^{φ+ψ}), [3]$$ where $$$Δ_1=δ_1+s$$$. The analytical expression of a dimensionless factor, $$$η^{''}$$$, is shown in Fig.2.

Methods

Image acquisition: DW imaging experiments were performed on a 3T GE MR750 scanner. A TRSE sequence shown in Fig. 1 was used to acquire DW images from six healthy human brains. A total of 15 b-values (0₁, 10₁, 20₁, 50₁, 100₁, 200₂, 400₂, 700₄, 1000₄, 1500₈, 2000₈, 2500₁₆, 3000₁₆, 3500₁₆, 4000₁₆ s/mm², with the subscripts denoting the NEXs, was used. Trace-weighted images were obtained to minimize the effect of diffusion anisotropy. The other sequence parameters were δ₁=10.8ms, δ₂=23.1ms, s=6.9ms, TR/TE=4200/106ms, reconstructed matrix size=256×256, slice thickness=3mm, scan time=24 minutes.

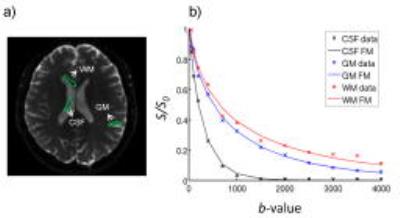
Analysis: The multi-b-value DW images were fitted to Eq.[3] to estimate the FM parameters, D_φ,ψ, φ, ψ, by using a non-linear least squares algorithm. The FM parameters were evaluated in specific regions of interest (ROIs) in gray matter (GM), white matter (WM), and cerebrospinal fluid (CSF) as shown in Fig.3a.

Results

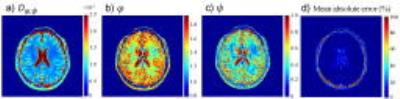
Figure 3b illustrates the agreement between the signal attenuation and the fitting curves using the FM model on the ROIs given in Fig.3a. Figure 4 summarizes the sample means ($$$\overline{x}$$$) and standard deviations (σ) of the FM parameters,D_φ,ψ, φ, ψ, as well as the mean absolute error (MAE) of the fitting in the three representative ROIs. The results showed that the FM parameters exhibited good contrast for the different tissues (i.e., different $$$\overline{x}$$$) as well as low variation within a tissue (i.e., σ). In addition, the MAEs ( $$$\overline{x}$$$ and σ) were small in all regions. These good performances were further illustrated in Fig. 5 where spatially resolved maps of D_φ,ψ, φ, ψ, and MAE obtained from voxel-by-voxel fitting of Eq.[3] for a representative subject is displayed. Both Figs. 4 and 5 illustrate that the FM model well described the diffusion signal obtained from a TRSE sequence.

Discussion and Conclusion

Acknowledgements

References

[1] Ingo C, Magin RL, Colon-Perez L, et al. On random walks and entropy in diffusion-weighted magnetic resonance imaging studies of neural tissue. Magn Reson Med. 2014;71(2):617–27.

[2] Karaman MM, Sui Y, Wang H, et al. Differentiating low- and high-grade pediatric brain tumors using a continuous-time random-walk diffusion model at high b-values. Magn Reson Med. 2015; 76:1149-1157.

[3] Magin RL, Abdullah O, Baleanu D, et al. Anomalous diffusion expressed through fractional order differential operators in the Bloch-Torrey equation. J Magn Reson Im. 2008;190:255–270.

[4] Zhou XJ, Gao Q, Abdullah O, Magin RL. Studies of anomalous diffusion in the human brain using fractional order calculus. Magn Reson Med. 2010;63:562–569.

[5] Sui Y, He W, Damen FW, Wanamaker C, Li Y, Zhou XJ. Differentiation of Low- and High- Grade Pediatric Brain Tumors with High b-Value Diffusion weighted MR Imaging and a Fractional Order Calculus Model. Radiology. 2015;277(2):489–496.

[6] Karaman MM, Wang H, Sui Y, et al. Fractional Motion Diffusion Model for Grading Pediatric Brain Tumors. Neuroimage Clin. 2016: 12:707-714.

[7] Fan Y, Gao JH. Fractional motion model for characterization of anomalous diffusion from NMR signals. Phys Rev E. 2015;92(1):012707.

[8] Reese TG, Heid O, Weisskoff RM, et al. Reduction of eddy-current-induced distortion in diffusion MRI using a twice-refocused spin echo. Magn Reson Med 2003;49:177–182.

[9] Eliazar II, Shlesinger MF. Fractional motions. Phys Rep. 2013;527(2):101–29.

[10] Hurst HE. Long-term storage capacity of reservoirs. Trans Am Soc Civ Eng. 1951;116:770-799.

[11] Gao Q, Srinivasan G, Magin RL, Zhou XJ. Anomalous diffusion measured by a twice-refocused spin echo pulse sequence: Analysis using fractional order calculus. J Magn Reson Imaging. 2011;33(5):1177-1183.