Synopsis

A generalized signal model for diffusional kurtosis imaging (DKI) is proposed containing an adjustable parameter that can be optimized to reduced systematic errors in kurtosis estimates. This is illustrated by applying an established tissue model for diffusion in brain to fix the parameter, and numerical simulations are employed to demonstrate the improvement in accuracy relative to kurtosis estimates obtained with the standard DKI signal model. Finally, in vivo brain data is used to compare mean kurtosis estimates obtained with the standard and optimized DKI signal models.

Purpose

Theory

The generalized DKI signal model is

$$S(b,\alpha) = S_{0}\exp\left\{\frac{3}{K(\alpha +1)} \left[ \left(1-\frac{\alpha DKb}{3}\right)^{(\alpha+1)/\alpha}-1\right]\right\},\tag{1}$$

where $$$S$$$ is the diffusion MRI signal magnitude, $$$D$$$ is the diffusivity, $$$K$$$ is the kurtosis, $$$b$$$ is the b-value, and $$$S_{0}$$$ is the signal for $$$b = 0$$$. For the special case $$$\alpha = 1$$$, this reduces to

$$S(b,1) = S_{0}\exp\left(-Db + \frac{K}{6}D^2b^2 \right),\tag{2}$$

which is the standard DKI signal model based on a truncated cumulant expansion¹. For other choices of $$$\alpha$$$, Eq. (1) corresponds to alternative signal models. To third order in the b-value, the cumulant expansion for Eq. (1) is

$$\ln\left[S(b,\alpha)\right] = \ln\left[S_{0}\right]-bD+\frac{K}{6}D^2b^2+(\alpha-1)\frac{K^2}{54}D^3b^3+O(b^4).\tag{3}$$

Note that $$$\alpha$$$ only enters through the cubic term of Eq. (3). Adjusting $$$\alpha$$$ therefore alters the third (and higher) order terms of the cumulant expansion, which impacts the systematic errors for the kurtosis estimates. Such systematic errors depend on the range of b-values used for fitting Eq. (1) and typically grow with an increase in the maximum b-value employed.

The parameter $$$\alpha$$$ may be optimized by using a reference signal model corresponding to the diffusion dynamics for a medium of interest. As an example, we utilize here an established reference signal model for isotropic brain tissue, based on a two-compartment description of water diffusion with one compartment representing the intra-neurite space and the other compartment the extra-neurite space. The intra-neurite space has a diffusivity $$$D_i$$$ and a water fraction $$$f$$$, while the extra-neurite space has diffusivity $$$D_e$$$ and a water fraction $$$1-f$$$. The intra-neurite space is assumed to consist of water restricted to randomly-oriented thin cylinders, and diffusion in the the extra-neurite space is taken as Gaussian. The reference signal model is then

$$\DeclareMathOperator\erf{erf}S_{ref} = S_{0}\left[(1-f)\exp(-bD_e)+f\sqrt{\frac{\pi}{4bD_i}}\cdot {\erf }\left(\sqrt{bD_i} \right) \right],\tag{4}$$

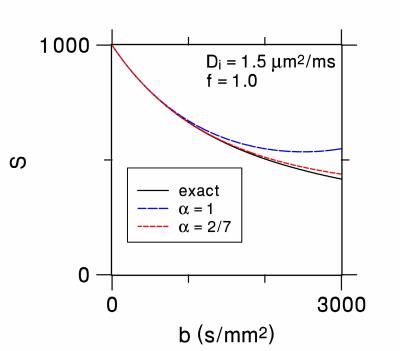
with $$$\DeclareMathOperator\erf{erf} \erf$$$ indicating the error function⁴. The cumulant expansion for Eq. (4) matches that of Eq. (3) to second order in the b-value provided $$$D$$$ and $$$K$$$ are the correct diffusivity and kurtosis for the brain tissue model, but the third order terms will, in general, differ. However, for $$$f=1$$$, the third order terms for the two expansions coincide if and only if $$$\alpha=2/7$$$. This then is a plausible choice as an optimal $$$\alpha$$$ value. Figure 1 compares the generalized DKI signal model for the standard $$$\alpha=1$$$ and the optimized $$$\alpha=2/7$$$ to the reference signal with $$$f=1$$$.

Methods

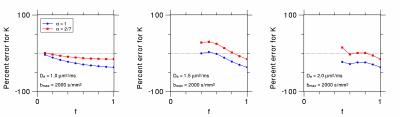
To compare the accuracy of kurtosis estimates for $$$\alpha=1$$$ and $$$\alpha=2/7$$$, we performed numerical simulations in which Eq. (1) was fit to Eq. (4) for 100 b-values ranging from 0 to 2000 s/mm². The intra-neurite water fractions varied from $$$f=0.1$$$ to $$$f=1.0$$$, and the extra-neurite diffusivity was either $$$D_e= 1.0,$$$ $$$1.5$$$, or $$$2.0$$$ μm²/ms. In each case, the intra-neurite diffusivity was calculated so as to make the total diffusivity $$$D = 1.0 $$$ μm²/ms.

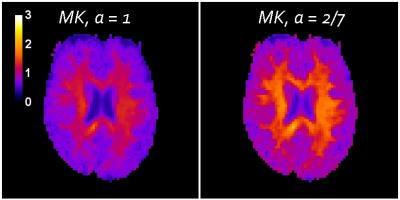
To demonstrate the effect of using the optimized $$$\alpha$$$ for human brain, conventional DKI data were acquired for one human subject on a 3T Trio MRI system using a twice-refocused diffusion-weighted pulse sequence. The b-values were 0, 1000, and 2000 s/mm² and 30 diffusion encoding directions were employed. Kurtosis estimate maps were obtained for each diffusion encoding direction by fitting Eq. (1) to the DKI data both with $$$\alpha=1$$$ and $$$\alpha=2/7$$$. Mean kurtosis (MK) maps were then generated by averaging the kurtosis estimate maps for all the diffusion encoding directions.

Results and Discussion

The percent errors of the kurtosis estimates for the numerical simulations are plotted in Fig. 2. For most of the cases considered, the optimized choice of $$$\alpha = 2/7$$$ results in smaller absolute errors than the standard $$$\alpha = 1$$$.

The MK maps are shown in Fig. 3. The MK with $$$\alpha = 2/7$$$ is about 25% higher than for $$$\alpha = 1$$$. The MK for the optimized signal model is potentially more accurate, especially in isotropic brain regions where Eq. (4) is most applicable. Improved accuracy of this type could be valuable for quantitative modeling of brain microstructure that utilizes the kurtosis as an experimental input, since errors in the kurtosis will affect the modeling predictions^2,3. However, if the kurtosis is simply used as a biomarker for diffusional non-Gaussianity, then either choice may serve equally well since they are highly correlated (r=0.985).

Acknowledgements

References

1. Jensen JH, Helpern JA. MRI quantification of non-Gaussian water diffusion by kurtosis analysis. NMR Biomed. 2010;23(7):698-710.

2. Fieremans E, Jensen JH, Helpern JA. White matter characterization with diffusional kurtosis imaging. Neuroimage. 2011;58(1):177-188.

3. Hui ES, Russell Glenn G, Helpern JA, Jensen JH. Kurtosis analysis of neural diffusion organization. Neuroimage. 2015;106:391-403.

4. Jespersen SN, Kroenke CD, Østergaard L, Ackerman JJ, Yablonskiy DA. Modeling dendrite density from magnetic resonance diffusion measurements. Neuroimage. 2007;34(4):1473-1486.