1682
Spatial Registration of fMRI Data Using Functional Correlation Tensors1Guangdong Provincial Key Laboratory of Medical Image Processing, School of Biomedical Engineering, Southern Medical University, Guangzhou, People's Republic of China, 2Department of Radiology and BRIC, University of North Carolina, Chapel Hill, NC, United States
Synopsis
Inter-subject registration of functional MRI (fMRI) data is a key step for group analysis. Here, we propose a novel registration strategy that considers functional information from both gray matter (GM) and white matter (WM). This is achieved using functional correlation tensors (FCTs), which capture the local correlation of the BOLD signals. Features extracted from both GM and WM functional correlation
PURPOSE
Inter-subject fMRI registration is typically performed with the guidance of T1-weighted MR images1-3 due to their high spatial resolution and better anatomical contrast. However, functional regions are not necessarily consistent with the anatomical structures4. Therefore, the aligned anatomical structures do not necessarily imply the aligned functional regions. While more methods have been developed to directly take into account the fMRI data during registration, existing methods only utilize functional features extracted from cortical GM4-6. This results in inaccurate registration because the cortical GM is thin, highly curved, and accounts for only a fraction of the whole brain. In this work, we propose to perform registration using information from both GM and WM by using functional correlation tensors.METHODS
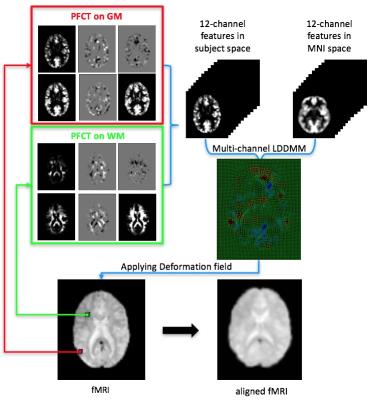
An overview of the proposed method is shown in Fig. 1. Our main contributions are as follows: (1) We propose a patch-based approach for computing the functional correlation tensor (PFCT) to extract the directional correlation information from resting-state fMRI data. (2) Guided by the probability maps of T1 MR images, PFCT is computed separately for GM and WM. (3) We show that functional registration can be improved by using a multi-channel LDDMM7 algorithm with PFCT features. Fig. 2 illustrates how PFCT is computed.RESULTS
Resting-state fMRI data of 20 healthy subjects were obtained from fcon_1000.projects.nitrc.org (New York data set B). Preprocessing includes slice timing, head movement correction, band-pass filtering of 0.01-0.1Hz, but no spatial smoothing. Further, head motion regression was performed using the Friston 24-Parameter Model. Affine registration to MNI space was finally performed using T1 MR images. We have validated our method by measuring the inter-subject consistency of default mode network (DMN) using independent component analysis (ICA) implemented by GIFT8.
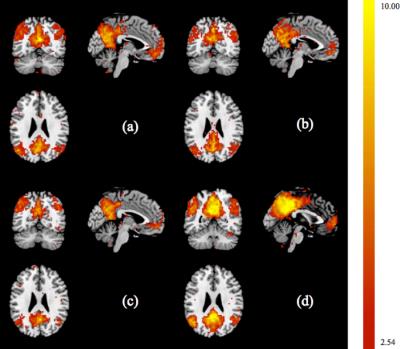
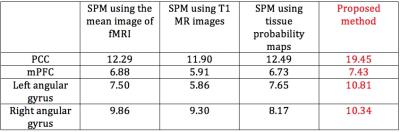
The inter-subject functional consistency of DMN can be measured by one sample t-test. Higher t value means higher functional consistency. Fig 3 shows our proposed method increased the maximum value of t-map to 19.45. Particularly, as shown in Table 1, four main components in DMN, including posterior cingulate cortex (PCC), medial prefrontal cortex (mPFC), and left and right angular gyrus, also increased the maximum values of t-map to 19.45, 7.43, 10.81, and 10.34.
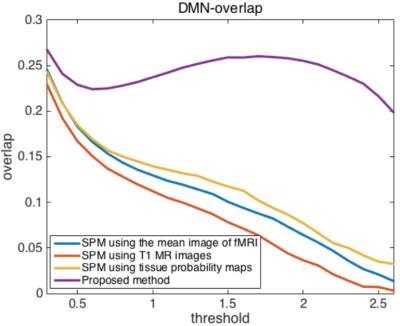
Finally, in Fig 4, we compare the overlap between each subject-specific DMN component and the group DMN component with different thresholds to generate binary images. The overlap of the DMN-related regions between each subject-specific DMN binary image and the group DMN binary image was computed as the intersection of A and B divided by the union of A and B, where A denotes the binary image of the group DMN and B denotes the binary image of one subject-specific DMN.
CONCLUSION
The experimental results have demonstrated that our proposed method can significantly improve functional image registration. This is largely due to the consideration of functional information from both GM and WM during the registration.Acknowledgements
No acknowledgement found.References
1. Ashburner, J. & Friston, K. J. Nonlinear spatial normalization using basis functions. Hum Brain Mapp 7, 254-266, doi:Doi 10.1002/(Sici)1097-0193(1999)7:4<254::Aid-Hbm4>3.0.Co;2-G (1999).
2. Ashburner, J. & Friston, K. J. Unified segmentation. Neuroimage 26, 839-851, doi:10.1016/j.neuroimage.2005.02.018 (2005).
3. Ashburner, J. A fast diffeomorphic image registration algorithm. Neuroimage 38, 95-113, doi:10.1016/j.neuroimage.2007.07.007 (2007).
4. Sabuncu, M. R. et al. Function-based Intersubject Alignment of Human Cortical Anatomy. Cereb Cortex 20, 130-140, doi:10.1093/cercor/bhp085 (2010).
5. Langs, G., Golland, P., Tie, Y., Rigolo, L. & Golby, A. J. Functional Geometry Alignment and Localization of Brain Areas. Advances in neural information processing systems 1, 1225-1233 (2010).
6. Jiang, D., Du, Y., Cheng, H., Jiang, T. & Fan, Y. Groupwise spatial normalization of fMRI data based on multi-range functional connectivity patterns. Neuroimage 82, 355-372, doi:10.1016/j.neuroimage.2013.05.093 (2013).
7. Zhang, P., Niethammer, M., Shen, D. G. & Yap, P. T. Large deformation diffeomorphic registration of diffusion-weighted imaging data. Medical image analysis 18, 1290-1298, doi:10.1016/j.media.2014.06.012 (2014).
8. Calhoun, V. D., Adali, T., Pearlson, G. D. & Pekar, J. J. A method for making group inferences from functional MRI data using independent component analysis. Hum Brain Mapp 14, 140-151, doi:Doi 10.1002/Hbm.1048 (2001).
Figures