1662
Dual-calibrated fMRI measurement of resting capillary and venous blood volumes1CUBRIC, Cardiff University, Cardiff, United Kingdom
Synopsis
The potential for dual-calibrated fMRI to provide quantitative estimates of physiological parameters has been increasingly investigated. We present a novel analysis methodology to estimate capillary (CBVcap) and venous (CBVv) blood volumes. These parameter estimates are made in addition to standard physiological parameters (cerebral blood flow (CBF), oxygen extraction fraction (OEF), and cerebral metabolic rate of oxygen (CMRO2)). Maps of CBVcap demonstrate a marked reduction in the appearance of large vessels (compared to CBVv data) and show significant correlations with CBF and CMRO2. These findings suggest an important role for CBVcap for assessing cerebral metabolic function and neurovascular coupling.
Purpose
A new analysis method to provide a non-invasive estimate of cerebral capillary blood volume from calibrated fMRI data.Methods
We have recently proposed a forward modelling method for the estimation of OEF using the dual-calibrated fMRI methodology1. This method allows for the simultaneous estimation of resting OEF, CBF, venous-weighted blood volume (CBVv) and CMRO2. In this work we incorporate flow-diffusion modelling of oxygen extraction2,3 to derive voxel-wise estimates of CBVcap. The modelling of oxygen extraction follows the work of [2] and [3]. The kinetics of oxygen extraction are based on extended Bohr–Kety–Crone–Renkin equations2, which are dependent on mean transit time (MTT = CBVcap/CBF), capillary transit-time heterogeneity (CTH) and the partial pressure of oxygen in the tissue (PtO2). The partial pressure of tissue oxygen is in turn modelled by Michaelis–Menten kinetics3 with a dependence on MTT and CTH. In this work we include the assumption of an idealised vascular network, such that CTH is linearly related to MTT (as observed in in-vivo measurements4). By cascading the kinetic models (under the assumption of an idealised vascular network), OEF is found to a have a monotonic relationship with MTT and can be fit with a rational equation (equation 1). Thus, the forward modelling approach can be re-parameterised in terms of resting CBF and CBVcap, rather than fitting for OEF.
$$$OEF=(1.01\cdot MTT-0.06)\diagup(MTT+3.34)$$$ Equation 1
where MTT is in units of seconds.
The
proposed analysis method was assessed in a cohort of 10 healthy volunteers.
Image data were acquired on a 3 T whole body MRI system. Functional data were
acquired using a pulsed arterial spin labelling (ASL) using a QUIPSS II
acquisition scheme. This sequence used a dual-echo gradient echo (GRE) readout
(TE1 = 2.7 ms TE2 = 29 ms, TR = 2.2 s, flip angle 90°,
FOV 22 cm, matrix 64 × 64, 12 slices of 7 mm thickness with an inter-slice gap
of 1 mm, TI1 = 700 ms, TI2 = 1500 ms). Respiratory challenges
consisted of 3 periods of hypercapnia
(5% CO2) and 2 periods of hyperoxia (50% O2)
interleaved with room air, for a total acquisition time of 18 minutes.
Results
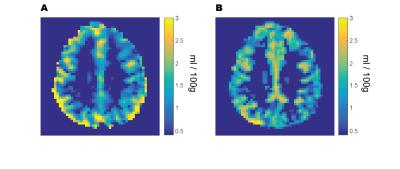
The mean grey matter capillary blood volume was found to be 1.61 ± 0.29 ml/100g, with a mean venous blood volume of 1.55 ± 0.16 ml/100g, representing a combined grey matter capillary and venous volume of 3.2 ml/100g and an approximately even volume distribution between capillary and venous compartments. The average grey matter MTT was 1.5 ± 0.22 seconds, corresponding to an OEF of 0.29 ± 0.03. The group mean grey matter CBF was 66.27± 18.6 ml/100g/min resulting in an average CMRO2 of 159.1 ± 32.3 μmol/100g/min. Maps of venous blood volume showed significant contributions from large veins (figure 1a), which were absent from maps of capillary blood volume (figure 1b). Across subjects grey matter values of CBVcap were correlated with CBF and CMRO2 (with corresponding R2 values of 0.78 and 0.96 p<0.001 for both relationships). CBVv was not significantly correlated with any other physiological parameter. As expected a strong correlation (R2 = 0.90, p<0.001) was found between CBF and CMRO2.Discussion
The high correlation between CBVcap and CBF is not un-expected due to the small variation in OEF and MTT (CBVcap /CBF) across subjects. The strong correlation of CBVcap with CMRO2 (slightly greater than between CBF and CMRO2) is perhaps surprising until we consider its relationship to CMRO2 in terms of the flow-diffusion model. Substituting the OEF model (Eq. 1) into the classic equation for CMRO2, we obtain the following relationship
$$$CMRO_{2}=Ca\cdot(CBF\cdot60)\cdot((1.01\cdot CBV_{cap}\diagup CBF-0.06)\diagup(CBV_{cap}\diagup CBF+3.34))$$$ Equation 2
where Ca is a constant representing the oxygen carrying capacity of a unit volume of blood, CBF is in units of ml/100g/second and CMRO2 is expressed in μmol/100g/min. Over a physiological range of MTT (1 to 2 seconds) equation 2 is well approximated by a linear equation (R2=0.99), equation 3.
$$$CMRO_{2}≈Ca\cdot(8.88\cdot CBV_{cap}+4.55\cdot CBF) $$$ Equation 3
Thus, we expect CMRO2 to be tightly coupled to CBVcap, and for measurements of CBVcap to be a good indication of oxygen metabolism. It is clear, under the assumptions of the model, that modulation of CBVcap (potentially through active control of pericytes5) would play a large part in determining the metabolic response to any stimulus.
Conclusions
The proposed method of measuring CBVcap takes advantage of existing data acquired during calibrated-fMRI experiments and well-known kinetic models to estimate a physiologically meaningful parameter. Initial evidence suggests that measurement of CBVcap could prove insightful for better understanding of physiological control of oxygen metabolism and neurovascular coupling.Acknowledgements
MG and RW acknowledge the support of the UK Engineering and Physical Sciences Research Council (EP/K020404/1) and the Wellcome Trust Institutional Support Fund for this work. AM acknowledges the generous support of the Cardiff University President’s Scholarships and RW thanks the Higher Education Funding Council for Wales support.References
[1] Germuska M., Merola A., Murphy K., Babic A., Richmond L., Khot S., Hall J.E., Wise R.G., 2016. A forward modelling approach for the estimation of oxygen extraction fraction by calibrated fMRI. Neuroimage 139, 313-323
[2] Jespersen S and Østergaard L. 2012. The roles of cerebral blood flow, capillary transit time heterogeneity, and oxygen tension in brain oxygenation and metabolism. JCBFM 32, 264–277
[3] Angleys H., Østergaard L., Jespersen S. 2015. The effects of capillary transit time heterogeneity (CTH) on brain oxygenation. JCBFM 35, 806–817
[4] Rasmussen P., Jespersen S., Østergaard L. 2015. The effects of transit time heterogeneity on brain oxygenation during rest and functional activation. JCBFM 35, 432-442
[5] Hall C., Reynell C., Gesslein B., Hamilton N., Mishra A., Sutherland B. O’Farrell F., Buchan A., Lauritzen M., Attwell D. 2014. Capillary pericytes regulate cerebral blood flow in health and disease. Nature 508, 55–60