Synopsis

3D-EPI is beneficial for real-time fMRI applications because the acquisition can be accelerated in both the in-plane and through-plane phase-encoded directions significantly increasing temporal resolution. Fully-sampled reference data are required in order to map coil sensitivities and unfold the aliased images that result. Acquiring these data with a segmented EPI readout matches the EPI-related distortions and dropouts between the un-accelerated reference data and the accelerated fMRI data. However, systematic differences in eddy-current-related phase between the segments can introduce errors during frequency offset correction (employed to correct for slow frequency drifts) unless accounted for. Here we present a simple correction scheme that greatly improves the tSNR of the time series.

Purpose

Real-time fMRI with neurofeedback requires a rapid sampling rate, which can be achieved using 3D-EPI¹ since partially parallel imaging (PPI)² can be employed in both the in-plane and through-plane phase-encoded directions. Coil sensitivity information is needed to unfold the aliased images that result. Since there are many potential sources of artefact, e.g. patient motion, high quality reference data is essential and a number of schemes for acquiring this data have been developed³. Acquiring reference data with the same EPI readout as the accelerated data matches the distortions between the two. In this case, an N-segment scheme is employed where N is the speed up factor in the in-plane phase-encoded direction. The EPI readouts are offset in time by 1/N of the echo-spacing along the phase-encoded direction⁴. By combining these segments, and fully encoding in the through-plane direction, a fully sampled volume can be constructed and coil sensitivities estimated.

Frequency-offset-correction is required in order to compensate for B₀ changes, e.g. due to breathing. Here we show that segment-related errors introduced by this frequency-offset-correction lead to artefact in the final images. The errors stem from systematic eddy-current-induced phase differences between the two segments, which are present in the navigator echoes due to their differential gradient history. However, these eddy currents are such that they have decayed by the time of the EPI readout making correction unnecessary. Therefore including these eddy-current effects inadvertently introduces a FOV/N Nyquist ghost into the reference data, which propagates through to the reconstructed images, reducing the tSNR and functional sensitivity of the time series. These ghosts are particularly problematic because the coil-sensitivity-errors coincide with the aliased locations of the signal that needs to be unfolded. Therefore, accounting for this effect and removing it from the frequency-offset-correction greatly improves image quality and tSNR.

Methods

Accelerated 3D-EPI data were acquired, with ethical approval, on a Siemens 3T Tim Trio as part of a real-time fMRI project, using 3 mm isotropic resolution and whole brain coverage. PPI in-plane (x2) and through-plane (x3) resulted in a volume TR of 1.2s. The aliased images were reconstructed using a real-time SENSE-based algorithm implemented as a Matlab (Mathworks, USA) plugin for Gadgetron⁵. To calculate coil sensitivities, fully sampled reference data were acquired, after the magnetisation had reached steady-state, by fully sampling in the through-plane direction and acquiring two EPI readout segments shifted by half the echo-spacing in the phase-encoded direction. When combined these data produced a fully-encoded k-space volume.

Standard frequency-offset-correction, in Hz, was based on the frequency difference between navigator echoes acquired at short echo time without phase-encoding via: δf = (Φ_{Nav 3} - Φ_{Nav 1}) / (2πΔt) where Φ_{Nav 3} - Φ_{Nav 1} is the phase difference between the third and first navigators, acquired with the same gradient polarity and a temporal separation of Δt. Differential gradient history, specific to each segment, led to differential eddy currents causing systematic phase differences between the segments (Fig.1). To address this, the amplitude-weighted mean phase difference between the two segments (across all partitions), which captures this systematic difference, was calculated. During the calculation of the frequency offset correction, half this value was subtracted from the phase difference of the first segment and half was added to the phase difference of the second segment. Subsequently, partition- and segment-specific frequency offset corrections were applied.

Results

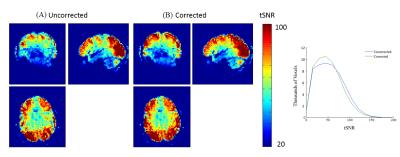
A schematic of the frequency offset with and without the proposed correction is shown in figure 1. Unaccounted for, this alternating segment-specific phase was captured by the frequency offset correction. The time constant of the eddy currents was such that they decayed by the time the EPI data were acquired. Therefore correcting for these effects inadvertently produced N/2 ghosts in the reference data that propagated through to the unaliased images and reduced the tSNR of the time series (Fig. 2A, C).

The proposed modified frequency-offset-correction, which removes the systematic difference in eddy-current-related phase accrual specific to the navigators, imparted improved phase consistency. As a result, the Nyquist ghost artefact was removed and the tSNR improved (Fig.2B, C).

Median tSNR was improved by 8%.

Conclusions

Acknowledgements

References

1. Lutti, A., Thomas, D. L., Hutton, C. & Weiskopf, N. High-resolution functional MRI at 3 T: 3D/2D echo-planar imaging with optimized physiological noise correction. Magn. Reson. Med. 69, 1657–1664 (2013).

2. Pruessmann, K. P., Weiger, M., Scheidegger, M. B. & Boesiger, P. SENSE: sensitivity encoding for fast MRI. Magn. Reson. Med. 42, 952–62 (1999).

3. Setsompop, K., Feinberg, D. A. & Polimeni, J. R. Rapid brain MRI acquisition techniques at ultra-high fields. NMR Biomed. in press (2016). doi:10.1002/nbm.3478

4. Feinberg, D. A. & Oshio, K. Phase errors in multi-shot echo planar imaging. Magn. Reson. Med. 32, 535–539 (1994).

5. Hansen, M. S. & Sørensen, T. S. Gadgetron: An open source framework for medical image reconstruction. Magn. Reson. Med. 000, 1–9 (2012).