Introduction

Diagnostic evaluation of in vivo human spine structures (cervical, thoracic, and lumbar; called as C-T-L) is important for assessing pathologies using crucial imaging tool, particularly MRI. However, it is difficult to acquire the whole C-T-L spine image at once due to the limited field-of-view (FOV) of receiver coil system.^1-3 Thus, deformable image registration method that made a single image through the separate images was widely used to perform the combining images, effectively.^3,4 In this study, we applied Scale Invariant Features Transform (SIFT) algorithm to C-T-L spine MR image for deformable registration of them to investigate the feasibility and reproducibility.

Method

MRI data acquisition: Five male healthy subjects (mean age ± standard deviation: 26 ± 2.1 years) participated in this study. Each part of C-T-L spine images were acquired with Philips 3.0 T MRI system (Achieva 3.0 T; Philips Medical Systems, The Best, Netherlands) using FSE sequence (image parameters: TE/TR=120/3,000 ms, FOV=288 mm2, ETL=27, matrix size=576 × 576, slice thickness=4.4 mm, and number of slices=5). Data processing: The SIFT algorithm was used to detect the feature points created from an edge or corner of an object for vector calculation. The SIFT algorithm was applied in five steps; detection of the extrema in scale-space, keypoint localization, keypoint orientation assignment, Generation of keypoint descriptor and Point matching process.⁵ In the case of multi-slice images, the point selection is only performed at the most central slice among them, and other slices are combined with the selected point at the most central slice to register images. For quantitative comparisons between the registered images using SIFT algorithm and commercially mounted algorithm in MRI system, we performed Bland-Altman analysis,⁶ and calculated Normalized Mean Square Error (NMSE) and Pearson’s correlation coefficients. These quantitative analysis procedures performed with images from MRI system. Note that there is no gold standard or ground truth for stitching image results, we assumed that the registered images from commercial MRI system as a reference images for quantitative analysis in this study.

Results and Discussion

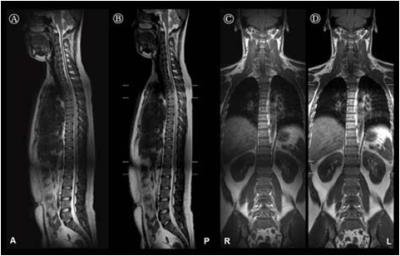
Fig.1 shows the comparative results, which are sagittal and coronal section images from representative subject, between the use of registered results with SIFT algorithm (A and C) and the use of deformable registration algorithm within the commercial MRI system (B and D). The calculated NMSE values from all subjects are represented 1.74×10⁻⁴ ± 3.68×10⁻⁵ (sagittal) and 1.85×10⁻⁴ ± 2.92×10⁻⁵ (coronal). For statistical results performed with paired t-test between the use of the SIFT algorithm and commercially mounted algorithm, note that there is no significant differences in sagittal or coronal image sections. (all p > 0.05). Fig.2 shows the quantitative comparison of the mean signal intensities from whole registered images with SIFT and commercially mounted algorithms in each subject’s image slices (A and B), and Bland-Altman analysis results (C and D). Notably, the calculated Pearson's coefficient values (r) represent high correlations between two stitched results performed with SIFT algorithm and commercially mounted algorithm (r = 0.88; p < 0.001 for sagittal section; r = 0.86; p < 0.001 for coronal section). In addition, the signal intensities comparison results, which are located close to the y = x line, and high coefficients of determination values (R² = 0.95 for sagittal section; R² = 0.93 for coronal section) also clearly indicate that the feasibility and reliability for the use of SIFT algorithm to spine MR image deformable registration process. For the Bland-Altman analysis results, the mean differences and standard deviations are -104.48 ± 280.88 A.U., and -187.79 ± 315.78 A.U. for sagittal and coronal section results, respectively. The all differences between SIFT algorithm and commercially mounted algorithm are within the ranges of ±1.96 times the standard deviations of the means, and there are no significant biases at the sagittal and coronal section results.

Conclusions

We provided preliminary findings of the feasibility and the validity of the SIFT algorithm application to deformable registration for in vivo human spine images. As shown in the results, the algorithm could be performed well in the MR spine images. We believe that our approach could be extended to the other image deformable registration fields such as whole-body MRIs and other imaging modalities as well, and could be helpful for clinical applications and diagnosis improvements.

Acknowledgements

No acknowledgement found.