1552
Simulated reorientational correlation times of collagen-associated water1Research Unit of Medical Imaging, Physics and Technology, University of Oulu, Oulu, Finland, 2Medical Research Center, University of Oulu and Oulu University Hospital, Oulu, Finland, 3Department of Diagnostic Radiology, Oulu University Hospital, Oulu, Finland, 4Department of Applied Physics, University of Eastern Finland, Kuopio, Finland, 5Diagnostic Imaging Center, Kuopio University Hospital, Kuopio, Finland
Synopsis
Correlation times of molecular motions are fundamentally related to magnetic relaxation. We use molecular dynamics simulations to compute the reorientational correlation times of water molecules associated with a model collagen molecule. Our aim is to provide a reference independent of measurements of correlation times of water in articular cartilage. The results suggest that although the reorientation slows down close to the protein surface, the diffusion between the different water pools appears to render the average correlation times short as compared to a water molecule trapped close to the macromolecule.
Purpose
Precise and quantitative assessment of the status of articular cartilage in terms of physically meaningful parameters with MRI is very challenging. A multitude of quantitative methods exist, but only a few of those are specific to a certain constituent or property of the tissue. Correlation time, a parameter that describes the physical properties of molecular motions fundamental to magnetic relaxation could be such very specific parameter.1,2 The purpose of this study was to estimate the contribution of the reorientational motion of collagen-associated water molecules to the measured correlation times in articular cartilage using molecular dynamics simulations.Theory
Molecular dynamics simulation uses iterative methods to integrate the equations of motion for a set of atoms connected with a force field. The simulation results in an approximate trajectory for each atom in the system. The time-correlation function (TCF) of the reorientation of water molecules is computed from the trajectory as
$$C_{2}(t)=\langle P_{2}[\hat{\boldsymbol{u}}(t + t_0) \cdot \hat{\boldsymbol{u}}(t_0)] \rangle, \qquad (1)$$
where $$$\hat{\boldsymbol{u}}$$$ is the unit vector of orientation connecting the hydrogen atoms. $$$P_2(x)$$$ is the second order Legendre polynomial. The correlation time $$$\tau_c$$$ of water reorientation is the integral over the TCF:
$$\tau_c = \int_0^\infty C_2(t) dt. \qquad (2)$$
Modeling
Type II collagen is a significant constituent of articular cartilage and
other cartilaginous tissues.3 Here, reorientation of water molecules was studied using atomistic molecular dynamics simulations of bulk water and a fully solvated collagen-like peptide 1QSU.4 The triple-helical structure of the peptide is shown in Figure 1. Water was simulated using the TIP4P/2005 model, which is known to reproduce the reorientational correlation time of bulk water well.5,6 The simulations of both systems were run with NAMD7 software at constant temperature, T=300 K, and pressure, P=1 atm for at least 18 ns.
Results
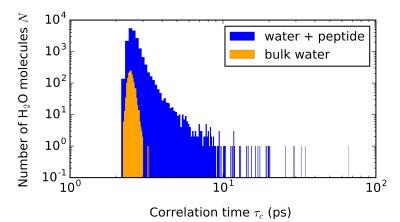
Reorientational correlation functions, as in Eq. 1, were computed from the simulated trajectories for each molecule using in-house Python scripts. On average, the orientational relaxation of the water molecules is very similar in each of the studied systems. Numerically integrated correlation times for bulk water and the water with 1QSU were $$$\tau_c=$$$2.48 ps and 2.71 ps, respectively. The longer correlation time in the latter results from the water-peptide interaction. This contribution was estimated with a monoexponential fit to the tail of the TCF for the water surrounding the peptide. The fit revealed a component with a time constant on the order of 0.1 ns. Figure 2 shows the distribution of $$$\tau_c$$$ in the water with the peptide and in bulk water. As can be seen from the figure, the vast majority of the water molecules have a short bulk-like 2-3 ps correlation time in both systems. In the 1QSU system, much longer $$$\tau_c$$$:s are also present, although only a few molecules have $$$\tau_c$$$ exceeding 20 ps.Discussion
Because of the diffusion between the protein-bound and
bulk water, the simulated correlation times represent a mixture of
water behavior in these two domains. The same kind of behavior could
be seen for e.g. water exchanging between bulk and the surface of a
collagen fibril. In more restricted spaces, such as inside the collagen
matrix, the reorientational motion could be much
slower. In the future we aim to use MD simulations
of $$$\tau_c$$$ to complement and substantiate the experimental $$$\tau_c$$$ measurements in articular cartilage and other musculoskeletal tissues.1Conclusions
Our data shows that water reorientation slows down in the vicinity of a collagen-like peptide. The exchange between bulk and the protein-bound water reduces the overall correlation times. This calls for studies of water reorientation in a more restricted environment, such as inside a collagen fibril or within a collagen meshwork with realistic fibril density.3,8Acknowledgements
Jane and Aatos Erkko Foundation as well as the Academy of Finland (grants #285909 and #293970) are gratefully acknowledged for financial support. CSC - IT Center for Science provided the computational resources.
References
1. Hanni M., Nissi M J, Rautiainen J, et al. Determination of correlation time in articular cartilage by T1rho relaxation dispersion, Proceedings of the International Society for Magnetic Resonance in Medicine. 2015; 23: 0117.
2. Elsayed H, Hanni M, Rautiainen J, Nissi M J, Nieminen M T, Correlation Time Mapping of Degenerated Human and Bovine Articular Cartilage Reveals Tissue Structure and Degenerative Changes, Proceedings of the International Society for Magnetic Resonance in Medicine. 2016; 24: 3003.
3. Fratzl P. Collagen: Structure and Mechanics. Springer Science & Business Media, 2008.
4. PDB ID: 1QSU. Kramer R Z, Venugopal M G, Bella J, et al. Staggered Molecular Packing in Crystals of a Collagen-like Peptide with a Single Charged pair. J. Mol. Biol. 2000; 301(5): 1191–1205.
5. Abascal J L F, Vega C. A general purpose model for the condensed phases of water: TIP4P/2005. J. Chem. Phys. 2005; 123: 234505.
6. Vega C, Abascal J L F. Simulating water with rigid non-polarizable models: a general perspective. Phys. Chem. Chem. Phys. 2011; 13: 19663–19688.
7. Phillips J C, Braun R, Wang W, et al. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005; 26: 1781–1802.
8. Denisov V P, Halle B. Protein hydration dynamics in aqueous solution. Faraday Discussions 1996; 103: 227.
Figures