1531
Alternating Direction Method of Multipliers for Diffusion Basis Functions (DBF)1Centro de Investigacion en Matematicas AC, Guanajuato, Mexico
Synopsis
We propose a new framework to solve the Diffusion Basis Functions model based on the alternating direction method of multipliers. We present an iterative, simple and efficient algorithm with closed-form updates. The proposal introduces a new regularization term to promote sparsity in the number of estimated fibers. Our experimental result shows that diffusion dictionary approaches benefit from our proposal.
Purpose
We present a new approach to solve the DBF model to estimate the axonal bundle orientations in vivo brain from DW-MRI. DBF1 models the DW-MR signal as a linear combination of diffusion basis functions (dictionary), $$$s_i = \sum_{j} \alpha_j \Phi_{i,j}$$$; where $$$\Phi_{i,j} = s_0 \exp \left( -b g_i^T T_j g_i \right)$$$ is the diffusion weighted signal value associated to the gradient $$$g_i$$$ and the base tensor $$$T_j$$$. Although the DBF model is an accurate procedure, it has been reported that it is prone to overestimate the number of fibers2. Successful approaches3,4 based on the DBF model have focused on adapting the fixed dictionary. These methods have overcome the limitations of the DBF model at the expense of complex subroutines to update the dictionary during execution. Our proposal avoids these complex subroutines by construing a more complete dictionary and deriving an efficient algorithm. This strategy is closer to the original idea of the DBF.
Method
To avoid the necessity of updates of the dictionary during the algorithm we generate a dictionary to consider more extensive set of orientations and different diffusion profiles compared to3,4. Fig 1 depicts how a completed dictionary is constructed. Increasing the dimension of the dictionary leads to a more complex optimization problem and tends to overestimate the number of fibers in the solution. Thus, we need an efficient algorithm that favors sparsity. The DBF method is formulated as a non-negative least squares (NNLS) problem $$$min \; \; \| s - \Phi \alpha \|_2^2 \; \; s.t. \; \alpha \geq 0$$$. To construct a more general framework we formulate the DBF problem as:
$$ \underset{}{\text{min}} \; \;D \left( s | y \right) + \mu R \left( \alpha^+ \right) \\\text{s. t.} \; \; y = \Phi \alpha \\\alpha = \alpha^+ \\\alpha^+ \geq 0 \\ $$
where $$$D(s|y)$$$ is a distance metric and $$$R(\alpha^+)$$$ is a regularization term. The purpose behind this formulation is to decouple the problem, so they can be optimized coordinate-wise and linked to each other through the constrains. To promote sparsity, we propose a regularization term that approximates the $$$\ell_0$$$-norm with $$$R(\alpha^+) = \sum_{i} 1 - \exp \left(-k\alpha^+_i \right)$$$. The term $$$R(\alpha^+)$$$ will tend to the total number of non-zero $$$\alpha^+$$$ as $$$k \to \infty$$$, penalizing the number of active elements in the linear combination. To solve this optimization problem, we use the Alternating Direction Method of Multipliers (ADMM)5 which handles the constraints by optimizing the augmented Lagrangian:
$$ \mathcal{L}_\rho (y,\alpha,\alpha^+, \lambda_1, \lambda_2) = D\left( s | y \right) + \mu R\left( \alpha^+ \right) + \lambda_1^T \left( y - \Phi \alpha \right) + \frac{\rho}{2} \| y - \Phi \alpha \| _2^2 + \lambda_2^T \left( \alpha - \alpha^+ \right) + \frac{\rho}{2} \| \alpha - \alpha^+ \| _2^2 $$
A general algorithm can be constructed by alternatively optimizing $$$\mathcal{L}_\rho$$$ with respect to each of the primal variables, followed by a gradient ascent in each of the dual variables. To obtain closed-form updates, we must define which distance metric and regularization term are going to be used. Existing work has focused on combining Euclidean Distance (ED) $$$d(s|y)=\sum_{i} \frac{1}{2} \left(s_i - y_i \right)^2$$$, and $$$\ell_1$$$-norm. The inconvenience of ED is that it assumes Gaussian distribution for the data. Because we are working with non-negative data, it is more natural to work with the Kullback-Leibler Divergence (KL) $$$d(s|y) = \sum_{i} s_i \log \frac{s_i}{y_i} - s_i + y_i$$$. In Fig 2, we define a specific algorithm using the KL divergence and our proposed $$$\ell_0$$$-norm approximation. From this algorithm we observed that the closed-form updates involve just matrix-vector operations.
Experiments
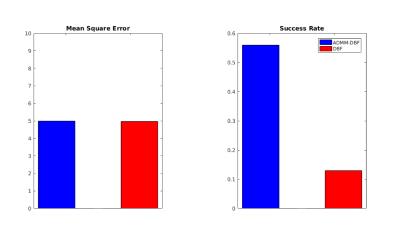
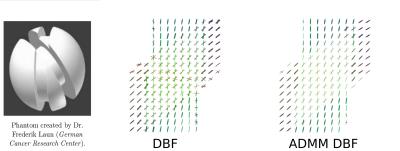
We compare our proposal described in Fig 2 and DBF method. \textbf{Synthetic Data}. We simulate a synthetic multi-shell data for one voxel with two fiber bundles at a crossing angle of 45-degrees. Fig 3 shows the intermediate solutions of each method. At the end of the iterations our proposal successfully recovers only two fiber bundles. \textbf{Physical Phantom}. This experiment was performed with the multi-shell data acquired on a single slice of a physical phantom available from the Sparse Reconstruction Challenge for Diffusion MRI 2014, SPARC dMRI 2014. Fig. 4 shows the Mean Square Error and Success Rate of the signal fitting. Fig. 5 depicts the computed voxel structure; we can see that our proposal describes more accurately the fiber intersection.Conclusions
Recent work based on DBF have focused on updating the fixed dictionary to obtain a better fitting. In this work, we presented a new framework to solve the DBF model that avoids complex optimization problems. The results show how the DBF model and dictionary based methods can benefit from our proposals.Acknowledgements
No acknowledgement found.References
[1] Ramirez-Manzanares A. et al. Diffusion basis functions decomposition for estimating white matter intravoxel fiber geometry. Medical Imaging, IEEE Transactions on, 2007 Aug;26(8):1091-102.
[2] Ramirez-Manzanares, A. et al. Resolving axon fiber crossings at clinical b-values: an evaluation study. Medical Physics, 2011 Sep;38(9):5239-53.
[3] Aranda, R. et al. Sparse and adaptive diffusion dictionary (SADD) for recovering intra-voxel whitematter structure. Medical Image Analysis, 26(1):243–255, Dec 2015
[4] Loya-Olivas, A. et al. LASADD: Linear acceleration method for adapting diffusion dictionaries. In ISMRM 23rd Annual Meeting and Exhibition, Toronto, Ontario, Canada, 2015
[5] Stephen Boyd, Neal Parikh, Eric Chu, Borja Peleato, and Jonathan Eckstein. Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends R in Machine Learning, vol. 3, no. 1, pp. 1–122, 2011.
Figures
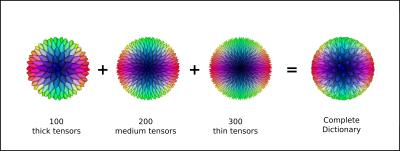


Fig 3. Reconstruction of two fiber bundles crossing during the iterations of the methods. Notice that our proposal leads to a more sparse solution.