1530
A Blind Deconvolution Approach to Fast MR T2 Mapping1Electrical Engineering, State University of New York at Buffalo, Buffalo, NY, United States, 2Shenzhen Institutes of Advanced Technologies, Shenzhen, People's Republic of China, 3Biomedical Engineering, State University of New York at Buffalo, Buffalo, NY, United States
Synopsis
MR parameter mapping has shown great potential but is still limited in clinical application due to the lengthy acquisition time. To accelerate the acquisition speed using multi-channel coils, we propose a novel blind deconvolution based approach to parameter mapping. The proposed method reconstructs the series of T2-weighted images, coil sensitivities of all channels, and the T2 maps simultaneously through a highly efficient, k-space based blind deconvolution approach. The experimental results show the potential of highly accelerated T2 mapping by the proposed method.
Purpose
MR parameter mapping has shown great potential but is still limited in clinical applications due to the lengthy acquisition time. Several reconstruction methods have been proposed to improve the acquisition speed 1-13. Some methods are based on the compressed sensing framework, where the T2-weighted image sequence is reconstructed using some sparsity or low-rankness prior information. Others directly reconstruct the T2 maps without the T2-weighted images. For multi-channel acquisition, the direct reconstruction method requires knowledge of coil sensitivities, which can be inaccurately estimated using the pre-scan. In this work, we propose a highly efficient blind deconvolution based approach to MR parameter mapping. Built on our recent work on Multi-Channel Blind Deconvolution (MalBEC)14, the proposed method reconstructs the series of T2-weighted images, coil sensitivities, and the T2 maps all at the same time.Theory and Methods
In MR parameter mapping, the m-th reconstructed image $$${I_m}$$$ is directly related to the acquisition at the m-th echo time and c-th channel as: $$${d_{m,c}} = {\Omega _m}{\cal F}{S_c}{I_m} + {n_{m,c}}$$$, where $$${\cal F}$$$ is the Fourier operator, $$${\Omega _m}$$$ is the specific undersampling pattern at m-th echo time, $$${S_c}$$$ represents the sensitivity for the c-th channel, and $$${n_{m,c}}$$$ denotes the k-space data noise. The image series $$${I_m}$$$ can be represented as$$${I_m} = \rho {e^{ - T{E_m}/{T_2}}}$$$ where $$$\rho $$$ is the proton density. In MalBEC, the acquired k-space data $$${d_{m,c}}$$$ is modeled as the circular convolution of $$${{\bf{s}}_m}$$$ (the k-space of $$${I_m}$$$) and the channel response function $$${h_c}$$$ (Fourier transform of coil sensitivities), that is $$${{\bf{d}}_{m,c}} = {{\bf{s}}_m}\circledast {{\bf{h}}_c}$$$. Because$$${I_m} = {e^{ - \Delta TE/{T_2}}}{I_{m - 1}}$$$, the k-space counterpart $$${{\bf{s}}_m}$$$ can also be modeled as $$${{\bf{s}}_{m + 1}} = {{\bf{s}}_m}\circledast {\cal M}$$$, where $$${\cal M}$$$ is the Fourier transform of $$${e^{-\Delta TE/{T_2}}}$$$. In MR parameter mapping, we wish to recover $$${\cal M}$$$, thereby $$${{T_2}}$$$, from undersampled data $$$\{{d_{m,c}}\} _{c = 1}^K$$$ without knowledge of $$$\{ {{\bf{s}}_m}\} _{m = 1}^M$$$ or $$$\{ {{\bf{h}}_c}\} _{c = 1}^K$$$. Apparently, the problem is ill-posed with non-unique solutions. We assume the channel response functions stay the same over different echo times. We then jointly solve for $$${{\bf{s}}_m}$$$, $$${{\bf{h}}_c}$$$, and $$${\cal M}$$$ using the following initialization and alternate minimizations.
Initialization: $$${{\bf{s}}_m} = {\cal F}\left( {sos\left( {{{\cal F}^{ - 1}}\left( {{\Omega ^{ - 1}}\left( {{d_{m,c}}} \right)} \right)} \right)} \right)$$$ where $$$sos$$$ represents the square-root-of-sum-of-square operation, and $$${\Omega ^{ - 1}}$$$ is the zero-filling procedure;
h step: $$${h_c} = \arg \mathop {\min }\limits_{{h_c}} {\sum\limits_m {\left\| {{d_{m,c}} - \Omega \left( {{{\bf{s}}_m}\circledast {h_c}} \right)} \right\|} ^2}$$$;
s step: $$${{\bf{s}}_m} = \arg \mathop {\min }\limits_{{{\bf{s}}_m}} {\sum\limits_c {\left\| {{d_{m,c}} - \Omega \left( {{{\bf{s}}_m} \circledast{h_c}} \right)} \right\|} ^2}$$$;
$$$\underline {\cal
M} $$$ step: $$${\cal M} = \arg \mathop {\min
}\limits_{\cal M} {\sum\limits_m {\left\| {{{\bf{s}}_{m + 1}} - {{\bf{s}}_m}\circledast {\cal M}} \right\|} ^2}$$$.
Results
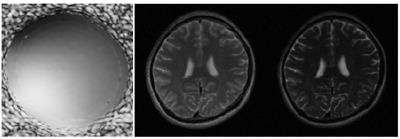
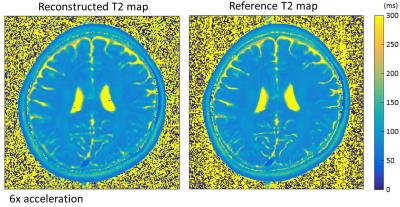
The proposed method was evaluated using a set of 8-channel T2 brain dataset from a 3T scanner(MAGNETOM Trio, SIEMENS, Germany) with a turbo spin echo sequence (matrix size = 192 x 192, FOV = 192 x 192 mm, slice thickness = 3 mm, ETL = 16, △TE = 8.8 ms, TR = 4000ms, bandwidth = 362Hz/pixel). The data were fully acquired and then retrospectively and randomly under-sampled (with sampling pattern in Ref. (15)) to simulate the accelerated acquisition with a reduction factor of 6. Figure 1 shows the reconstructed coil sensitivity map of the 1st channel, the reconstructed images at the first and last TEs from the proposed method. Figure 2 shows the reconstructed T2 map, which is compared against the reference T2 map obtained from the fully sampled data.Conclusion
A general blind deconvolution approach to MRI is proposed and applied on parameter mapping whereas the coil sensitivities, T2-weighted image series and the parameter maps are jointly reconstructed by alternate minimization. The reconstructed T2 maps have shown to be accurate, compared with the reference T2 maps, at high acceleration factors.Acknowledgements
This work is supported in part by the NSF CBET-1265612, CCF-1514403, NIH R21EB020861.References
[1] Cheng L, Stikov N, Ghugre N, Wright G. Practical medical applications of quantitative MR relaxometry, J. Magn. Reson. Imag., 36:805-824, 2012.
[2] Feng L, Otazo R, Jung H, Jensen J, Ye J, Sodickson DK, Kim D. Accelerated cardiac T2 mapping using breath-hold multiecho fast spin-echo pulse sequence with k-t FOCUSS. Magn. Reson. Med., 65:1661–1669, 2011.
[3] Velikina JV, Alexander AL, Samsonov A, Accelerating MR parameter mapping using sparsity promoting regularization in parametric dimension, Magn. Reson. Med., 70: 1263-1273, 2013.
[4] Huang C, Graff CG, Clarkson EW, Bilgin A, Altbach MI, T2 mapping from highly undersampled data by reconstruction of principal component coefficient maps using compressed sensing, Magn. Reson. Med., 67: 1355-1366, 2012.
[5] Petzschner FH, Ponce IP, Blaimer M, Jakob PM, Breuer FA. Fast MR parameter mapping using k-t principal component analysis, Magn. Reson. Med., 66: 706-716, 2011.
[6] Zhou Y, Shi C, Wang Y, Lyu J, Ying L, PRAIRIE: Accelerating MR Parameter Mapping Using Kernel-Based Manifold Learning and Pre-Imaging. ISMRM, 3585, 2015.
[7] Doneva M, Bornert P, Eggers H, Stehning C, Senegas J, Metins A. Compressed sensing reconstruction for magnetic resonance parameter mapping. Magn. Reson. Med., 64: 1114-1120, 2010.
[8] Li W, Griswold M, Yu X. Fast cardiac T1 mapping in mice using a model-based compressed sensing method. Magn. Reson. Med., 68:1127-1134, 2012.
[9] Zhao B, Lu W, Hitchens T.K, Lam F, Ho C, Liang ZP. Accelerated MR parameter mapping with low-rank and sparsity constraints. Magn. Reson. Med., 74:489-498, 2014.
[10] Zhang T, Pauly JM, Levesque IR. Accelerating parameter mapping with a locally low rank constraint. Magn. Reson. Med., 73:655–661, 2015.
[11] Sumpf TJ, Uecker M, Boretius S, Frahm J, Model-based nonlinear inverse reconstruction for T2 mapping using highly undersampled spin-echo MRI, J. Magn. Reson. Imag., 34: 420-428, 2011.
[12] Zhao B, Lam F, Liang ZP. Model-based MR parameter mapping withsparsity constraints: parameter estimation and performance bounds. IEEE Trans Med Imaging 2014;33:1832–1844.
[13] Peng X, Ying L, Liu Y, Yuan J, Liu X, Liang D. Accelerated exponential parameterization of T2 relaxation with model-driven low rank and sparsity priors (MORASA). Magn. Reson. Med., early view, DOI 10.1002/mrm.26083.
[14] Lyu J, Nakarmi U, Zhou Y, Zhang C, Ying L. Calibration-free Parallel Imaging Using Randomly Undersampled Multichannel Blind Deconvolution (MALBEC). ISMRM, 3232, 2016.
[15] Kim W, et al. Conflict-cost based random sampling design for parallel MRI with low rank constraints. SPIE Sensing Technology+ Applications. International Society for Optics and Photonics, 2015.