Synopsis

MR is a useful method for monitoring patients with pulmonary edema. To prevent difficult and costly transportation of patients to an MR imaging location, a portable magnet system was recently developed.The system necessarily operates in a noisy electro-magnetic environment,thus signal processing methods are needed to extract the NMR signal from a measurement system that is flooded with signal from external sources. This work compares a traditional adaptive filter theory approach against a sub-space projection approach. We demonstrate with phantom data measurements that these methods can improve detection of the NMR signal in anoisy environment.

Introduction

MR is well-suited for monitoring pulmonary edema, as the presence of fluid in the lung presents a sharp contrast in signal compared to healthy lungs. However, patients would be better served if one could move the imaging system to the patient. This work examines signal processing solutions to extract the NMR signal from a portable, unshielded, 88 Gauss NMR measurement system with a proton Larmor frequency of 374kHz¹.

Methods

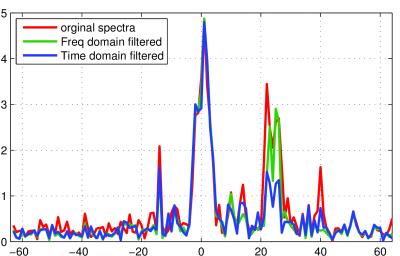
The Lung Density Monitoring (LDM) system is described by Dabaghyan et al¹. Two coils measured data, one for the NMR signal and the other placed ~1.25m away from the primary coil---close enough to sample the noise but far enough from the sample to pick up negligible signal from it. A CMPG sequence was used to induce an NMR signal from a water-filled 5-cm diameter spherical phantom positioned in the field's saddle point, with 32 echos after each excitation. 1000 repetitions were acquired, both with and without the phantom in place, while employing a 4-cycle RF phase-cycling pattern, to reduce systemic artifacts. 128 sample points were measured for each echo, yielding a data set of 128 x 32 x 1000 for each run. In a shielded environment, the NMR signal can be detected by computing the Fourier transform of a weighted average across echos and repetitions. If water is present in the field's saddle-point, the resulting spectra will show a peak at the center frequency, Fig~1.

In an unshielded environment, far-field electromagnetic sources dominate the measured signal in both the primary and reference coils. We examined 3 approaches to filter ambient noise in the primary coil. First, a frequency domain approach where with no phantom present, a weighting coefficient, $$$\alpha$$$, was computed to estimate the relative magnitude and phase between the coils. Then with the phantom in place, the $$$\alpha$$$ parameters were used to subtract the reference coil frequency signal from the primary coil signal.

Second, we employed a time-domain Least Mean Squared (LMS) adaptive filter². The measured NMR signal was treated as a 1D time-domain signal, and the spectrum of the filter output signal was computed. Third, we employed subspace projection to identify common signal elements across all echos and repetitions. With a data matrix, $$$A$$$---readout dimension along the rows and the echos+repetitions along the columns---the singular value decomposition (SVD)³ identified the most common components across readouts. With the SVD of $$$A$$$ defined as $$$A = U \Sigma V^H$$$, this produced matrices $$$U_{\mathrm{primary}}$$$ and $$$U_{\mathrm{reference}}$$$, each of size 128-x-128. To identify common components between the two columns, a cross-correlation of these matrices was performed, $$$X = U_{\mathrm{primary}}^H U^{\vphantom{H}}_{\mathrm{reference}}$$$. The readout components that appear in both coils show a high correlation index in the cross-correlation, $$$X$$$. Computing the average across blocks of 4-repetitions each prior to the SVD was beneficial in eliminating signal artifacts introduced by the sampling process. Phase-cycling in the CPMG pulse sequence ensured that these artifacts were out-of-phase. Averaging reduced artifacts significantly, and presented a cross-correlation matrix with two clear regions: a region with correlated signal, and a region with uncorrelated signal.

Results

The results of frequency-domain and time-domain filtering are shown in Fig. 2. The temporal-domain LMS filter performed slightly better than the frequency-domain filter, indicating external sources that vary in time. Neither filtering approach achieves spectra similar to the spectra from data collected in the shielded environment.

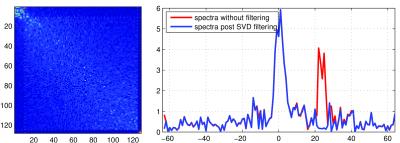
Fig. 3 illustrates the cross-correlation matrix derived from subspace processing. The upper left corner illustrates that the dominant components are also strongly correlated across coils. Then, the remaining signal components are predominantly uncorrelated---with lower magnitude and a diffuse character in lower right portion. The stark contrast between the correlated/uncorrelated regions provides a convenient location to threshold. This threshold can be used to filter away the strongest components of the primary signal, via $$$\widehat{A} = \widehat{U}_{\mathrm{primary}}^H \widehat{U}^{\vphantom{H}}_{\mathrm{primary}} A$$$ where $$$\widehat{U}$$$ contains columns of $$$U$$$ with an index larger than the threshold.

An example of the output after SVD filtering is shown in Fig 3, right, demonstrating a more effective approach than the previous frequency or temporal filters provided.

Conclusion

Acknowledgements

References

1. Dabaghyan M, Muradyan I, Hrovat A, Butler J, Frederick E, Zhou F, Kyriazis A, Hardin C, Patz S, Hrovat M. "A portable single-sided magnet system for remote NMR measurements of pulmonary function." NMR in Biomedicine 2014;27(12):1479–1489.

2. Haykin S. Adaptive Filter Theory. Prentice Hall, 3rd edition, 1996.

3. Horn RA, Johnson CR. Matrix Analysis. New York, NY: Cambridge University Press, 1985.