1522

SQUASHER: Slice quadratic phase with HSn encoding and reconstruction
Steen Moeller1, Xiaoping Wu2, Noam Harel2, Mike Garwood2, and Mehmet Akcakaya1

1Center for Magnetic Resonance Research, Minneapolis, MN, United States, 2University of Minnesota, Minneapolis, MN, United States

Synopsis

For 3D imaging, frequency-swept excitation can be used to obtain broad bandwidth and sharp slab profiles. The quadratic phase from such RF excitation imparts spatiotemporal encoding and can be leveraged for added encoding. Here we show that, by sliding the quadratic phase across the slice-encoding direction, synergy can be achieved when combining frequency-swept excitation with Fourier encoding, which has inherent optimal noise-properties.

Purpose

Brain MRI applications have been pushing for higher spatial resolution imaging, which requires trade-offs between scan time, SNR and resolution. 2D imaging has limited SNR as sub-millimeter imaging is pursued, requiring alternatives. 3D slab acquisitions offer higher SNR, but often require segmentation of data acquisition. The applicability of segmentation is hindered due to physiological and systematic limitations, such as motion-induced phase variations. Standard Fourier encoding makes it difficult to correct for such variations without additional calibration data due to the sharp fall-off of signal content in the slice-encoding direction [1]. Changes in RF pulse shapes have been proposed to tackle this challenge. In this study, we sought to take a different approach, based on quadratic phase modulation [2] along with 3D Fourier encoding to better distribute the signal content in the slice direction, and to enable higher acceleration rates robust to slice-undersampling with a modified reconstruction algorithm.

Methods

We conducted phantom and human experiments on a 7T Siemens scanner using the Nova single transmit, 32 receive head coil. A standard 3D FLASH sequence was modified such that stretched hyperbolic secant pulses (e.g., HS8) can be used for RF excitation. Note that when using HS8 pulses for excitation, the phase-encode gradients applied in the slice direction also shift the vertex of the quadratic, through-plane phase distribution of the resulting transverse magnetization. To demonstrate the utility of our method for high resolution imaging, we acquired 3D FLASH images using HS8 pulses. Relevant imaging parameters were FOV 256x256x30mm3, resolution 0.4x0.4x0.8mm3, TE/TR 21/39 ms, and nominal flip-angles 18 deg, 20% slab oversampling, in-plane undersampling (iPAT)=2. The ACS data were acquired with same imaging parameters but with 0.4x4.8x0.8mm3 resolution. To localize the signal along the slice direction and match the FOV resolution, the time-bandwidth product (or R value) of the HS8 pulse characterizing the shape of the quadratic phase was set to the number of phase encode steps in the slice direction. In this study, HS8 with R=60 (HS8R60) was used for phantom experiments whereas HS8R30 for the in-vivo experiments. For comparison, images using a standard sinc RF pulse were also acquired. For all acquisitions, maximal amount of gradient spoiling was applied to minimize the image artifact due to stimulated echoes. For acceleration along the kz dimension, a modified GRAPPA algorithm was developed. The algorithm removes the quadratic phase along kz (i.e. temporal spreading) of the signal prior to signal interpolation with GRAPPA and adds back the quadratic phase after signal interpolation. The mathematical description of the algorithm is given in Fig. 1.

Results

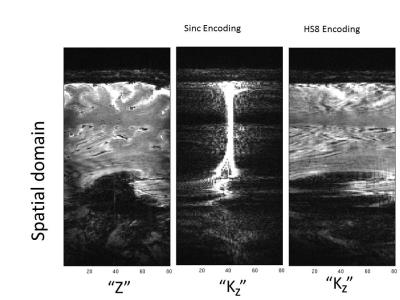
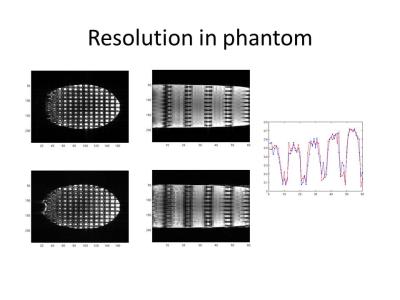
The {x,y,k_z} images acquired with the HS8 pulse presented more spread out signal content in the k_z dimension than did those with the sinc pulse which exhibited little signal content in outer k_z slices (Fig. 2). The proposed reconstruction effectively reconstructed images with 2D acceleration (ie, 2-fold in-plane and 2-fold through-plane acceleration) (Fig. 3), with comparable image quality to that with only 2-fold in-plane acceleration. Figure 4 shows results from two separate in-vivo acquisitions with sinc and HS8R30 excitation pulses respectively, and includes different retrospective slice-undersampling factors, as well as a low resolution reconstruction from the same dataset. At both resolutions, both standard Fourier encoding using a sinc pulse and our method using the HS8R30 pulse gave rise to good image quality when no slice acceleration was considered. However, the standard Fourier encoding method resulted in significant image degradation when additional slice undersampling was applied. By contrast, the proposed method using the modified GRAPPA reconstruction successfully maintained the image quality.

Discussion and conclusion

The use of frequency-swept pulses with high R values has been used to broaden the refocused encoded signal in a conventional GRE sequence, leading to a more even signal distribution in the hybrid (x,y,k_z) space. The acquired signal in {x,kz} is modulated with the quadratic phase from the excitation. By leveraging this knowledge, a modified GRAPPA algorithm has been proposed, allowing for slice-undersampling in the slab with limited spatial coverage, with little degradation in reconstruction quality at 2-fold acceleration.

The signal properties in hybrid space have direct spatial information, and this property makes the signal encoding different from conventional imaging and offers possibilities for self-calibration of the data, and correction of certain systematic and physiological imperfections for segmented acquisitions. The technique can find use for very high resolution acquisitions [3], enabling faster scanning and thus reduced occurrence of motion artifacts.

Acknowledgements

P41 EB015894, P30 ICC

References

[1] Wenchuan Wua, et al. High-resolution diffusion MRI at 7T using a three-dimensional multi-slab acquisition Neuroimage, Volume 143, December 2016, Pages 1–14

[2] Y. Shrot, L. Frydman Spatially encoded NMR and the acquisition of 2D magnetic resonance images within a single scan J Magn Reson, 172 (2005), pp. 179–190

[3] K. Setsompop et al. Generalized SLIce Dithered Enhanced Resolution Simultaneous MultiSlice (GSlider-SMS) to Increase Volume Encoding, SNR and Partition Profile Fidelity in High-Resolution Diffusion Imaging. ISMRM 2016, page 0607

Figures

Fig. 1. Equation for the proposed reconstruction algorithm, where kspmeas and ksprecon represents the measured and reconstructed kspace, r the in-plane spatial coordinates, z the through-plane kspace coordinate, Φ the quadratic phase of the signal, and GRAPPA the GRAPPA reconstruction.

Fig. 2. Reference image in the (x,y,z) space (left) and the images in the hybrid (x,y,kz) space obtained with sinc (middle) and HS8 (right) pulses. In each image, the horizontal axis is z or kz, which is the slice direction in the data acquisition. Note that the use of HS8 pulse for excitation resulted in more spread out signal content in the kz direction.

Fig. 3. (top row) reconstructed images without slice acceleration. (middle row) reconstructed images with 2-fold slice acceleration using the proposed modified GRAPPA reconstruction method. (bottom row) the signal variations along a line in the slice direction (red for without slice acceleration and blue for with slice acceleration). These data were acquired using an HS8 pulse with R=60.

Fig. 4. High resolution 3D flash brain images acquired with standard Fourier encoding and with the proposed method. The first two columns are with a sinc and HS8R30 excitation respectively with no kz acceleration (iPAT=2). The third column shows a sinc acquisition with GRAPPA reconstruction along the slice-direction, where the data is retrospectively undersampled in kz direction. The fourth and fifth columns are similarly reconstructed data for the proposed HS8R30 acquisition, with a standard GRAPPA reconstruction and the proposed modified GRAPPA reconstruction. The bottom row shows reconstructions of the same data with lower in-plane resolutions.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
1522