Synopsis

We propose a highly undersampled multi echo EPI sequence combined with a selfcalibrating reconstruction pipeline to adress offresonance artifacts. Ideas from the areas fieldmap, RPG and temporal subspace transform are combined yielding distortion free dynamic contrast images.

Introduction

Methods

Segmented multi-echo echo-planar imaging (SMEPI) experiments of one healthy volunteer were performed using a 3THDXT scanner (GE Healthcare, Waukesha, USA), with an 8-channel head coil (matrix=99x66, resolution=2.5mm isotropic, k-space line-spacing=576μs, TR=3s, 38 slices).

Each single SMEPI-shot (SSMEPI) comprised 9 echoes with alternating phase encoding polarity und undersampling factor 6 (Fig. 1a,b). The sampled k-space lines of all shots were interleaved with respect to each other such that each shot (distributed across the echoes) covers an overcomplete k-space and that 6 subsequent shots cover 9 complete echoes. Additionally, conventional single shot EPI images were acquired with similar parameters.

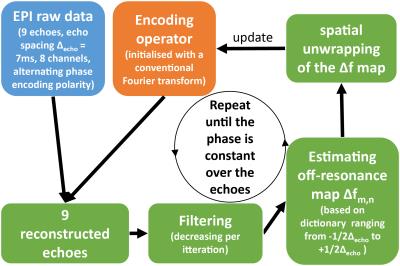
Two different reconstruction techniques are investigated. First, the fully sampled SMEPI data is reconstructed using iterative CG-SENSE. The forward operator F is given by the Fourier term, the coil sensitivities S_m,n,c of voxel m,n and coil c, the image signal I_m,n, a phase evolution term accounting for the off-resonance Δf_m,n and the time t_k,l when the k-space point K_k,l,c is acquired.

$$F(I)_{k,l,c}=K_{k,l,c}=\sum_{m=1}^M\sum_{n=1}^NI_{m,n}e^{-2{\pi}i(\frac{mk}{M}+\frac{nl}{N})}S_{m,n,c}e^{(2{\pi}i\Delta f_{m,n}t_{k,l})}$$

Fig. 2 illustrates the iterative algorithm where F itself is iteratively updated according to the calculated Δf_m,n. The off-resonance Δf_m,n is computed using a dictionary ranging from -1/(2Δ_echo)...-1/(2Δ_echo) where Δ_echo corresponds to the temporal spacing of two subsequent echoes (7ms).

The resulting Δf_m,n maps are unwrapped to account for values outside the dictionary window (aliasing). After 4 iterations, the phase of the echoes was almost constant and the magnitude images did not exhibit any noticeable shifts from echo to echo despite oposing phase encoding polarities (Fig. 2).

Second, a single shot reconstruction is adopted for SSMEPI data which uses the previously computed Δf_m,n and models the T2* decay with a temporal subspace Φ resulting in

$$K=F\phi\phi^HI=F\phi\alpha$$

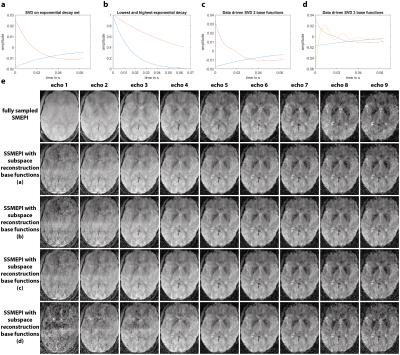
where α corresponds to the coefficients of the subspace. Several choices of subspaces were investigated including truncated SVD on a set of exponential functions, pure exponential functions and data-driven truncated SVD (Fig. 4a-d). Reconstruction time of one slice was about 8s and the off-resonance estimation required about 5s per slice (Matlab GPU implementations).

Results

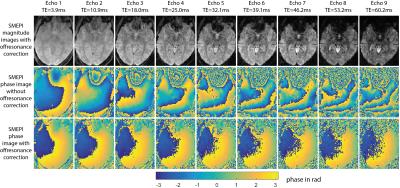
Fig. 3 depicts magnitude images of SMEPI and the corresponding phase images using conventional Fourier transform (second row) and using F (last row). After applying the algorithm from Fig. 2 the phase of all echoes was virtually constant and there was no apparent spatial mismatch between the echoes.

Fig. 4e compares synthesized SSMEPI images (subspace reconstruction) with the corresponding echoes of SMEPI for different subspaces (Fig. 4a-d). It is apparent, that the reconstruction fails independently from the subspace for the first echo, but the quality improves with TE and from echo 3 onwards the reconstruction achieves very reasonable results. There are very little differences between the first three subspaces (Fig. 4a-c) but the last subspace (Fig. 4d) falls short, most likely because there is insufficient information to fit 3 coefficients of the temporal base functions. An interesting observation is the oscillation of the third temporal base function in Fig. 4d (yellow line) which results from data driven truncated SVD. This indicates persistent magnitude fluctuations between odd and even echoes (no warping), probably caused by system imperfections (eddy currents etc.).

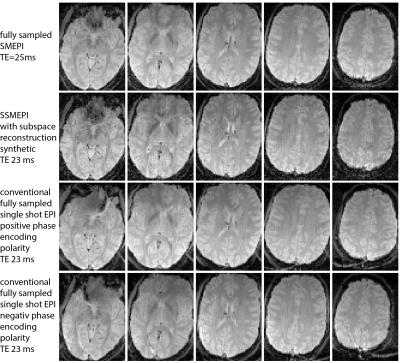
Fig. 5 compares SMEPI, SSMEPI and conventional EPI (both phase encoding polarities), all at similar TEs. All images exhibit very similar contrast but SSMEPI and SMEPI don’t suffer from off-resonance artifacts except for the extensive signal drop close to the nasal cavity. Conventional EPI exhibits significant distortions but outperforms SSMEPI in terms of SNR.

Discussion

Acknowledgements

References

[1] Jezzard, P. and R. S. Balaban (1995). "Correction for geometric distortion in echo planar images from B0 field variations." Magnetic Resonance in Medicine 34(1): 65-73.

[2] Andersson, J. L. R., et al. (2003). "How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging." Neuroimage 20(2): 870-888.

[3] Holland, D., et al. (2010). "Efficient correction of inhomogeneous static magnetic field-induced distortion in Echo Planar Imaging." Neuroimage 50(1): 175-183.

[4] Robson, M. D., et al. (1997). "Measurement of the point spread function in MRI using constant time imaging." Magn Reson Med 38(5): 733-740.

[5] Tamir, J. I., et al. (2016). "T2 shuffling: Sharp, multicontrast, volumetric fast spin-echo imaging." Magnetic Resonance in Medicine: n/a-n/a.