Synopsis

The SPIRIT parallel imaging algorithm was evaluated for use in a data rejection and replacement scheme to reduce motion artefacts.

Introduction

There have been several studies describing the use parallel imaging to identify and reject motion-artefacted data in MRI [1-4]. The idea is to separate the acquired data into two or more subsets, reconstruct them independently using SENSE [5] or GRAPPA [6] and then subtract them to reveal inconsistencies in k-space. A final image may be obtained by reconstructing the full dataset minus just the data identified as inconsistent. The method is capable of removing artefacts that come from isolated movements, such as coughing or swallowing.

There are some practical problems that limit the usefulness of the approach:

* Parallel imaging methods require calibration data to create coil maps (SENSE) or convolution coefficients (GRAPPA). If the calibration data is corrupted then the errors propagate through to the reconstructed images and it is difficult to identify true errors. Particularly for SENSE, a contiguous artefact-free region at the center of k-space is a prerequisite to perform FFTs.

* Many acquisitions already use speed-up mechanisms such as parallel imaging itself or partial Fourier to run in a reasonable scan time. If data are rejected in addition to those omitted to gain speed-up, then the effective sampling pattern in k-space will be patchy and non-uniform, especially in 3D datasets.

* To best identify inconsistent data it is important to make use of any possible redundancies in the data, such as conjugate symmetry, sparsity and spatial masking [2]. There needs to be a way to incorporate these various constraints into the reconstruction.

A parallel imaging method that may address these issues is SPIRIT [7]. SPIRIT enforces consistency in the reconstructed k-space by requiring that linear combinations of neighboring points sum to zero, which provides the basic test for inconsistency. Since the calibration of SPIRIT is performed in k-space, it does not do an FFT and hence does not require a contiguous region of uncorrupted data. Thus it can tolerate errors in the calibration data. Similarly, it does not depend on the sampling pattern of the raw data and can tolerate uneven gaps in the data. Lastly, since it is posed as an inverse problem, SPIRIT readily incorporate additional constraints.

These properties suggest that SPIRIT may be useful in the scheme to reject and replace motion-corrupted data based on data consistency. The purpose of the present study is to evaluate SPIRIT for the purpose of reducing motion artefacts.

Methods

MRI data were acquired on a 7T scanner (Siemens Magnetom) using a 32 channel head coil. A Cartesian data set of dimensions 320x320 was acquired with parallel imaging speed-up factor 2 (180 acquired lines in total). The raw data was taken offline for processing in Matlab.

SPIRIT proceeds in two steps: first the calibration and then the reconstruction. Both steps involve a linear equation and both are vulnerable to corrupt data. To add robustness to the presence of outlier-like errors, these equations were solved by iteratively reweighted least squares (IRLS) using the bisquare function. 10 iteration of IRLS were used. The IRLS penalizes high residual measurements by assigning them a low weight; a weight of zero means the data is rejected outright.

Reconstruction times for IRLS SPIRIT were around 10 minutes for this dataset.

Results and Discussion

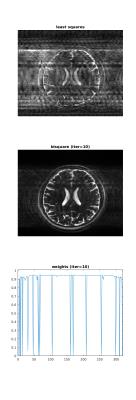
To test the ability to tolerate errors, phase errors corresponding to translational motion were imparted into the raw data. In the calibration region of 20 k-space lines, 10 were corrupted including 4 of the 5 center lines of k-space, and overall 33 out of the 180 lines were corrupted (18% in total).

The initial and final images are shown in Figure 1. Plotted underneath is the vector of weights for each phase encode on the final iteration. During the reconstruction the algorithm rejected 20 lines and assigned 1 line a very low weight (<0.1). The algorithm failed to reject 12 corrupt lines and wrongly rejected 1 uncorrupted line. Note that the bisquare function can be tuned to increase the sensitivity to errors, however this carries the risk of catastrophic failure if all the calibration data is rejected.

In conclusion, the properties of the SPIRIT algorithm indicate it is well-suited to this type of motion artefact reduction. Previous approaches using the same idea have been limited by one or more restrictions of the underlying parallel imaging methods, as outlined in the Introduction. Initial results are promising and the collection of clinical examples of motion-corrupted data in our lab for further evaluation is on-going.

Acknowledgements

References

1. Bydder M, Larkman DJ, Hajnal JV. Detection and elimination of motion artifacts by regeneration of k-space. Magn Reson Med. 2002 Apr;47(4):677-86.

2. Alexey A. Samsonov, Julia Velikina, Youngkyoo Jung, Eugene G. Kholmovski, Chris R. Johnson, and Walter F. Block. POCS-Enhanced Correction of Motion Artifacts in Parallel MRI. Magnetic Resonance in Medicine 63:1104–1110 (2010)

3. T.Nielsen and P.Börnert. Self-Consistency Driven Data Rejection for Reduction of Motion Artifacts. ISMRM SCIENTIFIC WORKSHOP: Motion Correction in MRI (2014)

4. Tom Hilbert, Tobias Kober, Jean-Philippe Thiran, Reto Meuli, and Gunnar Krueger. Phase-Encode Ghosting Detection using Multi-Channel Coil Arrays. ISMRM 2016:1829

5. Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: Sensitivity encoding for fast MRI. Magn Reson Med 1999;42: 952

6. Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. Generalized autocalibrating partially parallel acqusitions (GRAPPA). Magn Reson Med 2002;47:1202

7. Michael Lustig and John M. Pauly. SPIRiT: Iterative Self-consistent Parallel Imaging Reconstruction From Arbitrary k-Space. Magnetic Resonance in Medicine 64:457–471 (2010)