1515
Fast Multi-contrast MRI Super-resolution with Similar Anatomical Structure1Dept. of Electronic Science, Fujian Provincial Key Laboratory of Plasma and Magnetic Resonance, Xiamen University, Xiamen 361005, China, Xiamen, People's Republic of China, 2School of Mathematical Sciences, Xiamen University, Xiamen 361005, China, People's Republic of China, 3Dept. of Computer Science, Xiamen University of Technology, Xiamen 361024, China, People's Republic of China
Synopsis
Since magnetic resonance imaging (MRI) can offer images of an object with different contrasts, e.g., T1-weighted or T2-weighted, the shared information between inter-contrast images can be used to benefit super-resolution. Regarding the image as a locally stationary Gaussian process and using the least square method, we found weights of a local window are to be nearly invariant to image contrasts, which can be further used to transfer the shared information from one contrast to another. We analyze this property with comprehensive mathematics and numeric experiments. The reconstructed edges are more consistent to the original high-resolution image, indicated with higher PSNR and SSIM than the compared methods.
Introduction
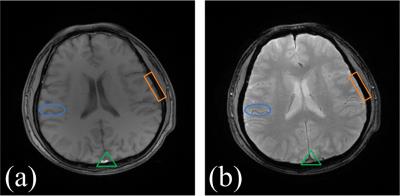
In magnetic resonance imaging (MRI), low-resolution images may be acquired and their resolutions can be improved by applying super-resolution methods 1, 2. MRI usually offer images of an object with different contrasts 3-5, e.g. T1-weighted or T2-weighted imaging (Fig. 1). Thus the shared information between inter-contrast images can be used to benefit super-resolution 3. In this paper, the local weight of image is found to be nearly invariant to image contrasts, which can be further used to transfer the shared information from one contrast to another. We analyze this property with comprehensive mathematics and numeric experiments.Method
Regarding image pixels as a locally stationary Gaussian process 6, the weights in a local window of high-resolution (HR) image can be calculated according to least square sense 6 $${\bf{b}} = {({{\bf{X}}^T}{\bf{X}})^{ - 1}}({{\bf{X}}^T}{\bf{y}})$$
where $$${\bf{X}}$$$ is a data matrix whose each row is composed of four nearest neighbors, $$${\bf{y}}$$$ is the central pixel and $$${\bf{b}}$$$ is the estimated weights.
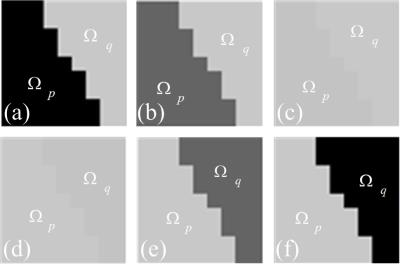
In this paper, the local regression weights are very similar among multi-contrast MRI images. For example, the weights in Fig. 2 are nearly the same. The same observation is also found in other synthetic and realistic MRI images. This property is analyzed with comprehensive mathematics and numeric experiments. By using the similar weights $$${\bf{b}}$$$, the target pixel \gamma of another contrast image is interpolated according to $$\gamma = {{\bf{b}}^T}{\bf{s}}$$
where the vector $$${\bf{s}}$$$ contains four nearest pixels in LR image around the interpolated point.
Results
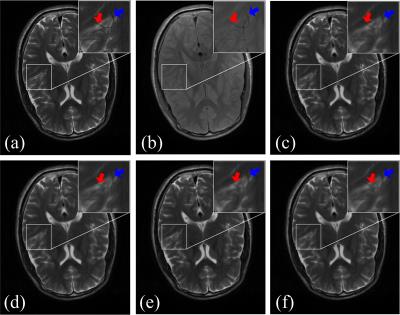
Experimental results on realistic MR images are presented in Fig. 3. The bicubic method produces many blocky artifacts and uncontinuity along edges. The edge-directed interpolation (NEDI) method 5 outperforms the bicubic method since sharper edges are observed in Fig. 3d. CGI 7 recovers the brain boundary in Fig. 4e much better than NEDI, but it still generates some uncontinuity along some edges. The new approach provides more consistent edges to the original HR image. The peak signal-to-noise ratio (PSNR), and structure similarity index (SSIM) 8 are employed to evaluate image quality. Higher PSNR and SSIM are achieved using the proposed method than the compared one.Conclusion
This paper presents a novel approach toward multi-contrast MRI image super-resolution by utilizing the shared weights of another contrast image. Experiment results demonstrate that the reconstructed edges are more consistent to the original high-resolution image.Acknowledgements
This work was supported by National Natural Science Foundation of China (61571380, 11375147 and 61302174), Natural Science Foundation of Fujian Province of China (2015J01346, 2016J05205), Fundamental Research Funds for the Central Universities (20720150109), Important Joint Research Project on Major Diseases of Xiamen City (3502Z20149032). The correspondence should be sent to Dr. Xiaobo Qu (Email: quxiaobo@xmu.edu.cn)References
1. Scherrer, B., et al., Super-resolution reconstruction to increase the spatial resolution of diffusion weighted images from orthogonal anisotropic acquisitions. Med. Imag Anal., 2012; 16(7):1465-76.
2. Poot, D. H. J., et al., Super-resolution for multislice diffusion tensor imaging. Magn. Reson. Med.,2013; 69(1):103-13.
3. Manjón, J. V., et al., MRI Superresolution using self-similarity and image priors. International Journal of Biomedical Imaging, 2010; 2010:1-11.
4. Qu, X., et al., Gaussian scale Mixture-based joint reconstruction of multicomponent MR images from undersampled k-space measurements, ISMRM’11, p 2838, 2011.
5. Qu, X., et al., Magnetic resonance image reconstruction from undersampled measurements using a patch-based nonlocal operator, Med. Imag Anal., 2014; 18(6):843-856.
6. Li, X., et al., New edge-directed interpolation. IEEE Trans. Image Process. 2001; 10(10):1521-27.
7. Z. Wei, et al., Contrast-guided image interpolation, IEEE Trans. Image Process. 2013; 22(11): 4271-4285.
8. Wang, Z., et al., Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process., 2004; 13(4):600-612.
Figures