1514
Accelerated Regularized Image Reconstruction in Spatiotemporal MRI1University of Minnesota, Minneapolis, MN, United States, 2Center for Magnetic Resonance Research, University of Minnesota
Synopsis
Interest in spatiotemporally-encoded MRI methods has increased over the last decade due mainly to their high tolerance to magnetic field inhomogeneities. However, the data acquired in spatiotemporal MRI can lead to challenging image reconstruction problems. In this abstract we propose a new framework for reconstructing images that leverages compressible structure in recent spatiotemporal encoding techniques to enable an iterative approximate inversion of the Bloch-equations for imaging. In particular, we can often obtain a visually indistinguishable reconstruction up to an order of magnitude faster than using the full inversion.
Purpose
In recent years, a number of spatiotemporally-encoded (SPEN) MRI techniques have been introduced that perform better than conventional Fourier imaging techniques in some situations, such as in single-shot imaging in the presence of large B0 inhomogeneity1,2,3. The initial sequences were hybrids of SPEN and k-space encoding strategies, whereas more recent methods such as STEREO (STEering REsonance over the Object) are solely based on spatiotemporal encoding4. Full 2D and 3D spatiotemporal encoding creates a challenge for image reconstruction because these non-Fourier techniques typically cannot leverage the frequency separation afforded in conventional Fourier encoding, and instead must use larger models to fully characterize the evolution of the spatially-dependent signals. For 2D encoding, the Bloch-simulation generated encoding matrix for an $$$N_1 \times N_2$$$ image with $$$M$$$ measurements is $$$M \times (N_1N_2)$$$. Using a least squares solution requires inversion of an $$$N_1 N_2\times N_1 N_2$$$ matrix, which can be prohibitively large (a 192x192 image with 30,000 samples requires over 15 GB of memory and hours of computing time). Using iterative techniques such as those central to contemporary regularization methods (e.g., sparsity, total variation, etc.) imposes significant additional computational demands caused by the repeated application of the encoding matrix and its adjoint. In this work we propose approximating the encoding matrix by the composition of two operators, which allows for a reduction in the effective size of the encoding matrix, and facilitates a new form of accelerated reconstruction.
Methods
Given an encoding matrix $$$A \in \mathcal{C}^{m \times n}$$$, found by numerically solving the Bloch equations, and measurements $$$b$$$ generated according to $$$Ax = b$$$ we would like to solve the regularized linear inverse problem $$x^* = \textrm{argmin} \| Ax - b\|_2^2 + \lambda \Omega(x) ,$$ where $$$x$$$ is a vectorized representation of the image and $$$\Omega(x)$$$ is a general regularizer. We are interested in size regimes where it is computationally difficult even to perform matrix-vector multiplications using the matrix $$$A$$$ (for example, size regimes where $$$A$$$ may not even fit in memory), and so even first-order methods are expensive. To circumvent this limitation and so that the overall approximate representation enjoys significantly reduced storage requirements, we approximate the matrix $$$A$$$ as the composition of two operators, each of which has low storage requirements and can be applied efficiently. In the case of some 2D spatiotemporal trajectories5, each row of $$$A$$$ is approximately sparse in the Fourier basis. Therefore, we decompose $$$A$$$ as $$$A\approx S \circ \mathcal{F}$$$ where $$$S$$$ is a sparse matrix and $$$\mathcal{F}$$$ is the Fourier operator. We can control the level of sparsity of $$$S$$$ by modifying the parameter controlling how close $$$\tilde{A}$$$ is to $$$A$$$. Note that applying both $$$\tilde{A}$$$ and $$$\tilde{A}^*$$$ to a vector is both space and memory-efficient via the FFT and sparse matrix multiplication which allows us to address the underlying optimization problem using first-order methods like FISTA6.Results and Discussion
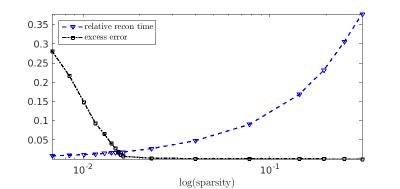
Figure 1 shows that the error dependence on sparsity decreases rapidly in the sparsity region where the computational speedup is large and only growing slowly. Because we can control the desired level of sparsity, this figure demonstrates that we can choose a level of sparsity for which the tradeoff between computational time and computational error is most beneficial. In particular, when the error from the approximation is on the order of the SNR of the system, there is no benefit to improving the approximation from $$$\tilde{A}$$$ to $$$A$$$. This curve shows that with less than 2% relative error, we can achieve 58x speedup compared to using the full matrix $$$A$$$ when applying the same iterative algorithm.
In Figure 2, we show example reconstructions using the full matrix versus using our fast decomposition with a sparsity level of 1.2% for different common regularizers. We solved the minimization problem using FISTA. Figure 2 also shows that our implementation results in reconstructions that are indistinguishable from the (computationally expensive) inverse solution but with a significant computational speedup.
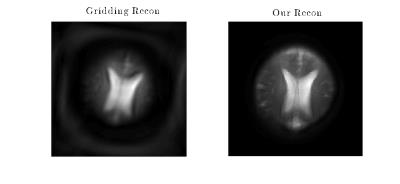
In Figure 3, we compare our method to gridding7. Although gridding produces a viable image an order of magnitude faster in this case, it is ill-suited for reconstructing data generated by a spatiotemporal method that lacks a k-space interpretation, such as STEREO.
Conclusion
In this abstract we propose a reconstruction framework for high-resolution scans based on computationally-efficient encoding matrix approximations. Our results demonstrate that this enables fast, visually accurate reconstructions from spatiotemporally encoded data. The approximation strategy developed here would extend to 3D image reconstructions, where direct inversion techniques are computationally intractable.Acknowledgements
This work is supported by NIH grants P41 EB015894, S10 RR027290, R24 MH105998, and by DARPA Young Faculty Award N66001-14-1-4047.
References
1. Shrot, Yoav, and Lucio Frydman. "Spatially encoded NMR and the acquisition of 2D magnetic resonance images within a single scan." Journal of Magnetic Resonance 172.2 (2005): 179-190.2. Chamberlain, Ryan, et al. "RASER: a new ultrafast magnetic resonance imaging method." Magnetic Resonance in Medicine 58.4 (2007): 794-799.
3. Ben-Eliezer, Noam, et al. "Parametric analysis of the spatial resolution and signal-to-noise ratio in super-resolved spatiotemporally encoded (SPEN) MRI." Magnetic Resonance in Medicine 72.2 (2014): 418-429.
4. Snyder, Angela LS, et al. "MRI by steering resonance through space."Magnetic Resonance in Medicine 72.1 (2014): 49-58.
5. Jang, Albert, et al. "2D Pulses using spatially dependent frequency sweeping." Magnetic Resonance in Medicine (2015).
6. Beck, Amir, and Marc Teboulle. "A fast iterative shrinkage-thresholding algorithm for linear inverse problems." SIAM Journal on Imaging Sciences 2.1 (2009): 183-202.
7. Pipe, James G., and Padmanabhan Menon. "Sampling density compensation in MRI: rationale and an iterative numerical solution." Magnetic Resonance in Medicine 41.1 (1999): 179-186.
Figures
Comparison of the (computationally intensive) reconstruction vs. our proposed approach for several different regularization functions. We also note that the storage of the full matrix requires 14.92GB, while our approximation of it requires only 230MB. We compare Tikhonov, Total Variation, and Wavelet sparsity regularizers.