1507
Signal Coding for SNR Multiplying Effect and Scan Acceleration Flexibility1Zhu Consulting, Scarsdale, NY, United States
Synopsis
In a way that augments existing encoding, signal coding promotes a multiplying effect of SNR and flexibility of scan acceleration. Its essence is to push for noise decimation by acquiring sums of marked signals from all components where the marking can be achieved by RF, gradient or other means. Its application to multi-slice MRI opens up a regime that enjoys both a √N SNR enhancement, as analogous to that of volumetric MRI, and flexibility with scan time budget, as equal or superior to that of existing multi-slice MRI.
Introduction
MR imaging entails mapping a target’s components spatially, spectrally or in a general parameter space. Some common MR approaches constrain the MR probing to one fraction of the components at a time. This tends to incur a cost in SNR. Multi-slice MRI is a notable example. A conventional multi-slice approach excites components of, and acquires signals from, one target slice at a time. While modern simultaneous multi-slice (SMS) approach1-3 probes NSMS slices at once, NSMS is up-bounded by the maximum slice-direction acceleration factor Rsmax practical with parallel MRI. This confines SMS also to a subset of components when N, the desired number of slices, is greater than Rsmax. The SNR scaling of either approach falls behind the curve as a result – as N increases, the scaling stagnates early on instead of tracking √total acquisition time 4. We propose a new approach that overcomes the SNR scaling barrier and demonstrate its ability to boost fast imaging.Methods and Results
In a way that augments existing encoding, the new approach promotes a multiplying effect of SNR and flexibility of scan acceleration. Its essence, hereby termed signal coding or echo composition, is to push for noise decimation by acquiring sums of marked signals from all components (Fig.1). The present work focuses on applying the new approach to multi-slice MRI.
The Fourier signal-coding strategy (Fig.2) gives rise to a full-fledged 3D k-space framework, one that supports analysis and practice of signal-coding SMS much the same way as a standard 3D k-space framework does for volumetric MRI. The framework suggests, for instance, i) acceleration along slice direction by skipping signal-coding steps, i.e., under-sampling k, causes aliasing or folding, ii) parallel MRI principle is readily applicable to effect acceleration in up to 3 dimensions simultaneously, and iii) there is considerable flexibility sampling the kx-ky-k space, options including, e.g., incorporation of random sampling and compressed sensing, addition of SMS’ view-to-view phase modulation, and implementation of non-Cartesian trajectories. Of particular significance, setting up multi-slice MRI in this framework ensues an SNR scaling analogous to that of volumetric MRI. In cases of even sampling in kx-ky-k, an analysis similar to that of SENSE5 gives signal-coding image SNR as:
SNRsc=SNRfull/(g√R)
where R is the product of in-plane and slice-direction acceleration factors, and SNRfull represents image SNR of a non-accelerated counterpart. Note that noise decimation and SNRfull scale with √N, a multiplying effect that allows SNRsc to track, within a g-factor penalty, √total acquisition time. This is in contrast to that of conventional multi-slice or modern SMS, where noise averaging and decimation is under-exploited for relatively large N. Modern SMS can be viewed as a special case where only k=0 is sampled and Rs is tied to NSMS (Rs=NSMS) – its SNR under-performs when practical Rs cannot reach N and it must repeat to cover N slices.
Signal-coding SMS was evaluated in simulation studies. k-space data corresponding to various multi-slice and kx-ky-k sampling configurations were synthesized based on a 32-channel volumetric data set from repository http://mridata.org. Sensitivity calibrations were performed separately using 12x12 center k-space. SENSE-type algorithms were used for image reconstructions.
A first study used a Fig.2C-type strategy, with spiral trajectories employed at each sampled k, to signal-code and spatial-encode 12 transaxial slices. The sampling involved under-sampling of outer kx-ky space (varying-density spirals) and 3x under-sampling of k (RF-based phase modulations). Signal-coding SMS yielded results (Fig.3C) that are in excellent agreement with the original (Fig.3A). In a further study targeting 12 coronal slices, the k-space sampling trajectory was composed of line segments parallel to ky. Sampling of kx-k used a pseudo-random pattern reflecting a 9x acceleration (Fig.3D). These two studies demonstrated incorporation of fast spiral trajectories, 3D acceleration, and random sampling spokes – signal-coding SMS promises to offer greater opportunities for rapid imaging than modern SMS does.
A third study used Fig.2C-type strategy to signal-code and spatial-encode multiple coronal slices, with Cartesian trajectories employed at each sampled k. Three evaluated cases indicated flexible tradeoffs between speed, N and SNR as enabled by signal-coding SMS (Figs.4 and 5). Notice in particular the SNR gain in accordance with √N (Fig.5) – this contrasts with modern SMS’ limited SNR multiplying effect.
Discussions
For many clinical multi-slice MRI protocols signal-coding SMS introduces a regime that enjoys both a √N SNR enhancement, as analogous to that of volumetric MRI, and flexibility with scan time budget, as equal or superior to that of existing multi-slice MRI. There can be other applications of the signal coding principle, leveraging the numerous mechanisms for manipulating spin dynamics and modifying MR signals.Acknowledgements
No acknowledgement found.References
1. Barth M, Breuer F, Koopmans PJ, Norris DG, Poser BA. Simultaneous Multislice (SMS) Imaging Techniques, Magn Reson Med 75:63-81, 2016.
2. Breuer FA, Blaimer M, Heidemann RM, Mueller MF, Griswold MA, Jakob PM. Controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA) for multi-slice imaging. Magn Reson Med 53:684–691, 2005.
3. Setsompop K, Gagoski BA, Polimeni JR, Witzel T, Wedeen VJ, Wald LL. Blipped-controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g-factor penalty. Magn Reson Med 67:1210–1224, 2012.
4. Macovski A, Noise in MRI, Magn Reson Med, 36:494-497, 1996.
5. Pruessmann KP, Weiger W, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI, Magn Reson Med, 42:952-962, 1999.
Figures

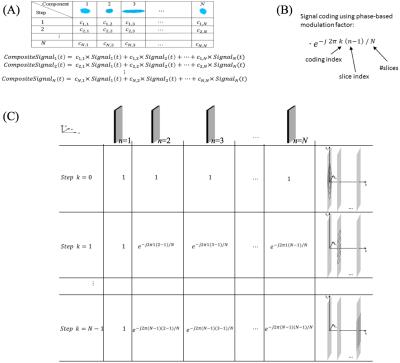
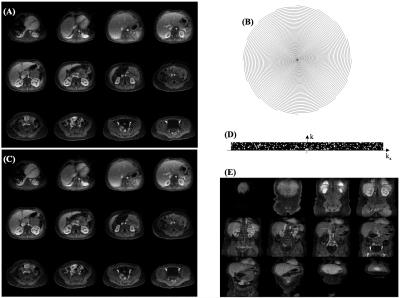
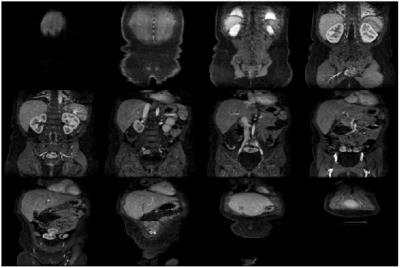
Fig.3 The first study targeted 12 slices of 19mm center-to-center spacing (A). The parallel receive data reflected 3x acceleration sampling k and a same 16-arm kx-ky spiral sampling trajectory for all four k steps (B). An iterative reconstruction led to resulting images (C). The second study targeted 12 coronal slices of 12mm center-to-center spacing. In this example the k-space sampling trajectory is composed of line segments parallel to ky (y=S/I). Sampling of kx-k employed a pseudo-random pattern reflecting a 9x acceleration (D). An iterative reconstruction led to resulting images (E).