1503

Blood saturation modeling in multiband multislab Time-of-Flight brain MRI
Alexis Amadon1, Gaël Saïb1, Nicolas Boulant1, and Alexandre Vignaud1

1DRF / I2BM / NeuroSpin / UNIRS, CEA-Saclay, Gif-sur-Yvette, France

Synopsis

Multiband multislab Time-of-Flight angiography has recently been proposed for reduced acquisition time and improved sensitivity in the human brain at 3T and 7T. However, in these previous studies, blood saturation has not been taken into account as blood traverses several slabs acquired simultaneously. Here a simple modeling of blood magnetization history is provided to take this saturation into account, which appears essential to avoid strong losses of blood to background signal ratio. Slab-dependent multiband-added VUSE pulses are simulated to counteract these losses both at 3T and 7T, from which a methodology is derived to optimize multiband TOF sequence parameters.

Purpose

Multiband multi-slab 3D Time-of-Flight magnetic resonance angiography has been proposed for reduced acquisition time and improved sensitivity in the human brain,1 in particular at Ultra High Field (UHF) where high resolution Maximum Intensity Projection (MIP) images are sought.2 The assumption implicitly made so far is that fresh blood enters the slabs acquired simultaneously. However, the partially-saturated magnetization of blood spins coming out of the acquired lower slab(s) does not have time to relax before entering a simultaneously-acquired upper slab. Therefore, as mentioned in a previous study,2 blood signal in the upper slab(s) is lessened with respect to that in the lower slab(s), and can even be destroyed if inappropriate acquisition parameters are selected. This work gives guidelines to correct for that approximate assumption and to optimize Time-Of-Flight (TOF) acquisition parameters given a targeted blood velocity.

Methods

TONE3 or VUSE4 pulses intend to maintain a constant fresh blood signal by ramping up the sequence of flip angles (FA) that blood magnetization experiences as arterial blood moves upwards through a slab. Wang et al.’s5 recursive algorithm for a spoiled gradient echo sequence (GRE) is used here to derive the ideal sequence of FA’s to be specified throughout the set of slabs acquired simultaneously, taking magnetization longitudinal regrowth into account between the slabs and assuming a constant blood flow velocity v along the z-axis (transverse to the slabs). Let FOVz be the total field-of-view along z, Ns the number of slabs to cover FOVz, Th each slab thickness (Th=FOVz/Ns), MB the multiband acceleration factor, TR the pulse repetition time, T1 the blood relaxation time (E1=e-TR/T1), M0 its thermal equilibrium magnetization, Ms,p (Ss,p) its longitudinal magnetization before (its signal after) RF pulse p in slab s, θs,p the pulse FA series experienced by blood in slab s (p={0...Np–1} with Np= ceil(Th/(v.TR)); s={0…Ns –1}), and θ=θ0,0. Three cases are considered to compute Ms,p depending on the RF pulse scheme: 1/ constant-FA simplification,6 2/ FA adjusted between slabs, 3/ constant blood signal enforcement with ideal VUSE pulses. Their computational model is given in Fig. 1.

For brain TOF acquisition, the blood signal should be enhanced with respect to that of the background white matter (WM) in steady state: the worst case WM signal is computed from SWM= maxs,p(MSSWM.e-TE/T2*.sinθs,p) where MSSWM is given in eq.2 with WM parameters in Table 1. Assuming FOVz=144 mm covers most human brains, two multiband scenarios were analyzed at 3T and 7T (using parameters in Table 1): {Ns=4, MB=2}2 and {Ns=9, MB=3}1.

Results and Discussion

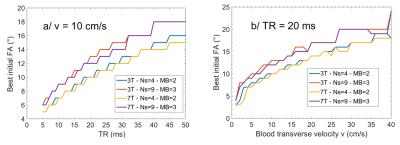
When considering the third case above, the Blood to WM signal Ratio BWR = Sblood/SWM is plotted as a function of the TOF sequence parameters θ and TR in Fig.2, at 3T and 7T. As can be seen from the “tidal waves” on the plots, this dependency hints that TR should be minimized while θ should be maximized. Nevertheless this can only be achieved if the blood velocity is not too small. Otherwise blood reaches the threshold where, before it comes out of the last multiband slab, its saturation can no longer be compensated by increasing the FA within the slabs (θNs-1,Np-1 in eq.3 must remain < 90°). Given v and TR, enforcement of a constant blood signal through multiband slabs then yields constraints on maximum θ. These constraints are represented by the blue wave crests for v = 10cm/s on Fig.2. Note how fairly constant BWR remains on those crests. Therefore TR should be chosen as small as possible with regards to SAR constraints. Then given a targeted v, the optimal θ can be found on the wave crest as in Fig.3a. For TR = 20ms, this initial FA is plotted in Fig.3b as a function of v in all four scenarios.

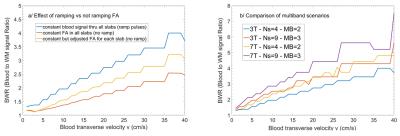
Now, as shown in Fig.4a, the relative BWR loss is important when using constant or slab-dependent FA settings rather than constant blood signal VUSE-pulse enforcement. At last, BWR is also represented as a function of v in all four scenarios for TR=20 ms in Fig.4b, which shows the MB=3 scenario should be favored over MB=2.

Conclusion

Blood saturation should not be ignored in multiband multislab TOF experiments, as it can lead to a 50% drop in blood to WM signal ratio. At least FA adjustment between multiband slabs should be considered. Moreover, whenever possible, slab-dependent ramp pulses should be added to generate optimal multiband TOF pulses so as to maintain an even contrast between arterial blood and brain parenchyma. A simple methodology was introduced to optimize multiband TOF sequence parameters, allowing in particular to specify slab FA ramps.

Acknowledgements

No acknowledgement found.

References

1. Schulz, J., Boyacioglu, R. and Norris, D. G. Multiband multislab 3D time-of-flight magnetic resonance angiography for reduced acquisition time and improved sensitivity. Magn. Reson. Med. 2016, 75: 1662–1668.

2. Schmitter S, Wu X, Moeller S, Auerbach EJ, Adriany G, Van de Moortele P-F, and Ugurbil K, Slab-selective pTX Multiband TOF Angiography at 7 Tesla, p. 542, proceedings ISMRM 2015, Toronto.

3. Aitkinson, D., et al. Improved MR angiography with variable flip angle excitation and increased resolution. Radiology 1994, 190:890-894.

4. Priatna, A. and Paschal, C. B., Variable-angle uniform signal excitation (VUSE) for three dimensional time-of-flight MR angiography. J. Magn. Reson. Imaging 1995, 5: 421–427.

5. Wang, S. J., Nishimura, D. G., and Macovski, A. Multiple-readout selective inversion recovery angiography. Magn. Reson. Med. 1991, 17:244-251.

6. Haacke, E. M., Brown, R. W., Thompson M. R., Venkatesan R., Magnetic Resonance Imaging: Physical Principles and Sequence Design, 1999, Wiley-Liss.

a. Herscovich P, Raichle ME. What is the correct value for the brain-blood partition coefficient for water?. J Cereb Blood Flow Metab 1985;5:65– 69.

b. Gutteridge, S. , Ramanathan, C., and Bowtell R., Mapping the Absolute Value of M0 Using Dipolar Field Effects, Magn. Reson. Med. 2002, 47:871-879.

c. Lu, H., Clingman, C., Golay, X. and van Zijl, P. C.M., Determining the longitudinal relaxation time (T1) of blood at 3.0 Tesla. Magn. Reson. Med. 2004, 52: 679–682.

d. Wansapura JP, Holland SK, Dunn RS, Ball WS. NMR relaxation times in the human brain at 3.0 tesla. J Magn Reson Imaging 1999;9:531–538.

e. Rane, S. D., Gore, J. C. Measurement of T1 of human arterial and venous blood at 7 T, Magn Reson. Imaging 2013, 31:477-479.

f. Bock, M. et al. Time-of-Flight MRA at 7 Tesla, MAGNETOM Flash, Siemens, Issue 2010, 1:74-78.

g. Gevers, S., van Osch, M. J., et al, Intra- and multicenter reproducibility of pulsed, continuous and pseudo-continuous arterial spin labeling methods for measuring cerebral perfusion, J Cereb Blood Flow Metab. 2011; 31(8): 1706–1715.

h. Peters AM, Brookes MJ, Hoogenraad FG, Gowland PA, Francis ST, Morris PG, Bowtell R. T2* measurements in human brain at 1.5, 3 and 7 T. Magn Reson Imaging, 2007; 25: 748–753.

i. Koush, Y., Elliott, M. A., and Mathiak, K., Single Voxel Proton Spectroscopy for Neurofeedback at 7 Tesla, Materials 2011, 4, 1548-1563.

j. Peters AM, Brookes MJ, Hoogenraad FG, Gowland PA, Francis ST, Morris PG, Bowtell R. Comparison of T2* Measurements in Human Brain at 1.5, 3 and 7 T, p. 926, proceedings ISMRM 2006, Seattle.

Figures

Table 1: Physical parameters used in this model. White matter is taken as the reference background tissue because it has the lowest T1 in the brain parenchyma (worst case). Regarding T2* relaxation, the echo time TE used for the spoiled Gradient Echo sequence simulation was 3.5 ms. Superscript letters correspond to references given in the Reference section.

Figure 1 : Computational model used to derive the arterial blood longitudinal magnetization and signal in TOF multiband sequences, considering three RF pulse schemes : 1/ constant-FA simplification, 2/ slab-dependent FA, 3/ constant blood signal enforcement with ideal VUSE pulses. See text for the definition of the symbols.

Figure 2: Blood to White Matter signal ratio (BWR) as a function of TR and flip angle at bottom slab entry θ, assuming blood signal can remain constant through the set of slabs. The blue wave is the region where a ramp of FA is applicable to make this assumption valid when v = 10 cm/s. Beyond, saturation makes blood signal drop before the end of the top slab. In each of the four scenarios, the BWR remains fairly constant on the blue wave edge, which should favor short TR and θ values if acquisition speed is an issue.

Figure 3: Flip angle at bottom slab entry θ yielding the largest BWR in the four scenarios: a/ as a function of TR for v = 10 cm/s (cf. blue wave crest in fig.2), b/ as a function of v for TR = 20 ms. Interestingly, the 3T and 7T values are practically identical, so field strength should not be an issue in the determination of θ for the TOF sequence designer.

Figure 4: BWR as a function of v, computed with best θ corresponding to TR = 20 ms (cf. Fig.3b), a/ at 3T, in the Ns=4, MB=2 scenario. The BWR loss induced by not using VUSE pulses remains almost constant, around 50% if the FA is kept the same throughout all slabs, and 30% if it is adjusted between slabs; b/ in the four multiband scenarios. Note BWR is almost identical in the conditions {3T, Ns=9, MB=3} and {7T, Ns=4, MB=2}. Although Signal-to-Noise is not taken into account, this shows the MB=3 scenario should be favored over MB=2 whenever possible.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
1503