1498

Phase Encoding with Bloch-Siegert effect using Parallel Transmit
Yuqing Wan1, Maolin Qiu1, Gigi Galiana1, and R. Todd Constable1,2

1Radiology & Biomedical Imaging, Yale School of Medicine, New Haven, CT, United States, 2Neurosurgery, Yale School of Medicine, New Haven, United States

Synopsis

A gradient-free, Bloch-Siegert effect based nonlinear spatial encoding scheme was introduced for silent scanning and to eliminate gradient-induced eddy currents in conventional MRI. We implemented a phase encoding scheme with a parallel transmit system on a 7T scanner to demonstrate feasibility. As a proof of concept, we demonstrated that B-S RF pulses can easilty produce nonlinear spatial encoding for MR imaging. The SAR limitations at 7T limit the efficiency of the encoding, but suggest the feasibility of this approach at lower fields.

Introduction

A gradient-free, Bloch-Siegert effect based nonlinear spatial encoding scheme1 was introduced for silent scanning and to eliminate gradient-induced eddy currents in conventional MRI. The previous study primarily focused on spatial encoding theories and simulation experiments. Based on these findings, we further implemented a phase encoding scheme with a parallel transmit system on a 7T scanner to demonstrate feasibility.

Methods

In the presence of an off-resonance RF field, an additional Bloch-Siegert precession is induced with frequency: $$$\omega_{BS}=\frac{(\gamma{B_1})^2}{2\omega_{RF}}$$$, when $$$ \omega_{RF}>>\gamma{B_1}$$$, where $$$\omega_{RF}$$$ is the off-resonance frequency shift, $$$B_1$$$ the local RF strength and $$$\gamma$$$ the gyromagnetic2. The Bloch-Siegert frequency $$$\omega_{RF}$$$ depends on the spatially varying $$$B_1$$$ field and therefore can be exploited to encode the image in a similar way to traditional gradient based encoding. Unlike previous RF encodings3,4, Bloch-Siegert shifts naturally generate nonlinear encoding with different $$$B_1$$$ fields delivered from selected channels of an existing RF phased array1. In this configuration, different levels of current ($$$A_c$$$) are applied to individual channels to create distinctive $$$B_1$$$ fields ( $$${B_1}(r)=\sum{{A_c}\cdot {B_{1c}}(r)}$$$), resulting in distinguishable phase maps for spatial encoding. With these nonlinear phase encodings, the images can be reconstructed using nonFourier-based algorithms as done with other nonlinear encoding strategies5-8.

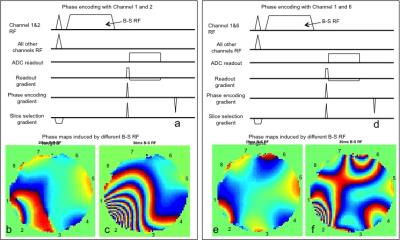
To demonstrate the phase changes induced by Bloch-Siegert effect, we designed a gradient-echo-like pulse sequence with Fermi pulses inserted between excitation and encoding (Figure 1 (a) and (d)). The B-S RF pulse is applied with an off-resonance frequency of 4kHz with variable durations to produce different amounts of phase winding. With a parallel transmit system, we specify the B-S RF pulse applied on specific channels to create unique phase mappings. The 2D images in this study are acquired with a spherical phantom in a 7T scanner and 8-channel parallel transmit/receive head coil (TR=3s, TE=44.4ms, slice thickness of 5mm, matrix size 64x64, FOV=150mm).

The acquired phase maps are used to reconstruct a numerical phantom. Forty different channel combinations were selected for spatial encoding, each with 128 B-S RF pulse durations spanning 20-40ms. Data from all 8 receive channels was used for parallel imaging.

Results

As shown in Figure 1, distinctive phase maps are created by the B-S RF pulses applied on different RF channels. By changing the length of these pulses, phase is unwound or wound up (Figure 1 (b) vs (c) and (e) vs (f)). This is similar to conventional encoding where phase accumulates through time while phase encode gradients are applied. By selecting different transmit channels to apply B-S RF, we change the spatial shape of these unique encoding patterns (Figure 1 (b) vs (e) and (c) vs (f)). Therefore, each image voxel is assigned a signature phase evolution through time, that can be recovered with a nonlinear image reconstruction algorithm. Figure 2 (b) shows the reconstructed images using these encoding phases with numerical phantoms.

Discussion

In this study, we demonstrated the feasibility of nonlinear spatial encoding with B-S RF pulses. By specifying RF pulses of different lengths on certain channels, distinguishable phase maps are created. These phase maps were used to reconstruct an image. While the image is blurred in the center, overall image quality is excellent. Resolution is lower in the center because the phase change at the center is slower than that in the peripheral regions for the encoding patterns used, similar to the gradient strength affecting image resolution in conventional imaging. We can potentially optimize for large $$$B_1$$$ at the center for more efficient encoding with in-phase excitation from all channels. Such an optimized encoding scheme is currently under development to mitigate these effects.

It is also worth noting that this study is primarily limited by the specific absorption rate (SAR) issue at an ultra-high field scanner (7T), which is the only system with parallel transmit available to the authors. This work at 7T does not imply we advocate for this method at 7T but it allows us to prove feasibility with a parallel transmit system. Within such a high field, the maximum $$$B_1$$$ strength is limited and the encoding efficiency is compromised. To assess this effect, we simulated an image reconstruction with the same SAR level at 3T (approximately twice the $$$B_1$$$ strength). The image was reconstructed with less blurring and smaller features were discernable, supporting the feasibility of B-S encoding at lower fields.

Conclusion

Using parallel transmit with 7T scanner, we demonstrated a proof of concept that B-S RF pulses can easilty produce nonlinear spatial encoding for MR imaging. The SAR limitations at 7T limit the efficiency of the encoding, but suggest the feasibility of this approach at lower fields.

Acknowledgements

$$$ $$$

References

1. Wan Y., et al, Nonlinear RF spatial encoding with multiple transmit coils based on Bloch-Siegert shift, ISMRM 2016 5822.

2. Sacolick, L.I., et al., B1 mapping by Bloch-Siegert shift. Magn Reson Med, 2010. 63(5): p. 1315-22.

3. Kartasch, R., et al., Spatial phase encoding exploiting the Bloch-Siegert shift effect. Magnetic Resonance Materials in Physics Biology and Medicine, 2014. 27(5): p. 363-371.

4. Cao Z., et al, Frequency encoding by Bloch-Siegert shift, ISMRM 2014 4220.

5. Stockmann, J.P., et al., O-space imaging: Highly efficient parallel imaging using second-order nonlinear fields as encoding gradients with no phase encoding. Magn Reson Med, 2010. 64(2): p. 447-56.

6. Tam, L.K., et al., Null space imaging: nonlinear magnetic encoding fields designed complementary to receiver coil sensitivities for improved acceleration in parallel imaging. Magn Reson Med, 2012. 68(4): p. 1166-75.

7. Galiana, G. and R.T. Constable, Single echo MRI. PLoS One, 2014. 9(1): p. e86008.

8. Hennig, J., et al., Parallel imaging in non-bijective, curvilinear magnetic field gradients: a concept study. Magnetic Resonance Materials in Physics Biology and Medicine, 2008. 21(1-2): p. 5-14.

Figures

Figure 1. To create encoding phase maps, a Fermi shaped B-S RF pulse is applied to certain transmit channels after the slice selection pulse, followed by normal Cartesian encodings and readouts. The phase encoding B-S RF pulse is applied to channel 1 and 2 on the left panel, and to channel 1 and 6 on the right panel. (a) and (d) demonstrates the timing diagram. (b) and (e) are the phase maps with the B-S pulses applied for 20ms and (c) and (f) with the pulses for 30ms, showing that the phase winding accumulations through time.

Figure 2. Using 40 different encoding patterns, each with 128 B-S RF pulses ranging 20 to 40ms, we simulated the reconstruction of a numeric phantom (a). The computed image at 7T (b) shows large features of the phantom, but resolution towards the center is lower than that of the peripheral regions. This is primarily due to insufficient encoding with lower limited by the SAR guidelines. We also simulated encodings at 3T with twice B1 intensity (equivalent SAR level) and the improved result is shown in (c), suggesting that the B-S RF encoding is feasible at lower fields.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
1498