1491
Determination of the Optimum Pattern Length of MRF SequencesKarsten Sommer1, Thomas Amthor1, Peter Koken1, Jakob Meineke1, and Mariya Doneva1
1Philips Research Europe, Hamburg, Germany
Synopsis
An important open question in magnetic resonance fingerprinting (MRF) is the optimal choice of sequence parameters, i.e. the ideal length and shape of the pattern that defines the variation of the acquisition parameters. Here we apply a Monte Carlo based measure of sequence performance to find the optimal flip angle pattern for different pattern lengths. Afterwards, the most efficient pattern is found by evaluating these optimized sequences’ actual performance in phantom experiments using various acceleration factors.
Purpose
Magnetic resonance fingerprinting (MRF) is a new approach to tissue parameter quantification that has recently gained much attention in the MR community1. In this method, unique signal evolutions are created by varying the acquisition parameters throughout the scan. Afterwards, the acquired data are matched to a dictionary of all possible signal evolutions to obtain the tissue parameters of the sample. An important open question in MRF is the optimal choice of sequence parameters, i.e. the ideal length and shape of the pattern that defines the variation of the acquisition parameters. In this contribution, we use a recently proposed measure of sequence performance2 to find the optimal flip angle (FA) pattern for different pattern lengths. Afterwards, the most efficient pattern is found by evaluating the sequences’ performance in phantom experiments using various acceleration factors.Methods
The encoding capability of gradient-spoiled SSFP-like sequences3 was evaluated using a recently proposed Monte Carlo method2 for fifty equidistant T1/T2 combinations (T1 range: 200-1500 ms; T2 range: 50-400 ms). To simulate artifacts due to undersampling, randomly resampled signal-dependent noise with an amplitude of approximately 10% of the signal was repeatedly (niter=2000) added to both the real and imaginary part of the complex signal evolutions. The resulting curves were matched to a dictionary consisting of the closest adjacent entries2. Afterwards, the average T1/T2 errors of the matches were calculated. This method was then applied to evaluate the performance of MRF sequences with constant TR=15 ms but varying random FA patterns (range: 0-60°) that were created using an adapted noise spectrum to suppress high frequencies. Three different cut-off frequencies were used, each applied to generate 500 random patterns (1500 in total), to allow for both quickly and slowly varying FA pattern shapes. This procedure was carried out for six different pattern lengths L (100, 250, 500, 1000, 2000, and 3000 RF shots). For each pattern length, the FA pattern with the lowest total error was employed in an MRF phantom study to find the highest suitable acceleration factor R. To this end, MRF measurements of a gel tube phantom containing 12 substances with various T1/T2 combinations in the range of the dictionary were performed on a Philips Achieva 3T scanner with an 8-channel head coil using the six optimal FA patterns and various values of R (range: 1-30). A uniform density spiral readout and a relaxation interval of 3000 ms between pattern repetitions was employed in all cases. In addition, reference T1 and T2 maps were obtained using an inversion recovery scan with 5 different inversion times (range: 50-2050 ms) and a multi-echo TSE scan with 20 echoes (TE range: 32-352 ms), respectively. The RMSEs of the MRF-derived T1 and T2 values in the tubes relative to the average values in the reference maps (ΔT1,ΔT2) were calculated. The efficiency of the MRF scans was defined using a metric similar to the one proposed by Deoni et al.4: $$$\Lambda_i=\frac{\overline{T_i / \Delta T_i}}{\sqrt{T_{acq}}}$$$, where $$$i=1,2$$$ and the average refers to the different values in the 12 tubes. The acquisition time $$$T_{acq}$$$ was calculated without taking the relaxation interval between pattern repetitions into account because this ‘waiting time’ could be used for data acquisition in another slice.Results and Discussion
Figure 1 depicts the optimized
FA patterns for the six different pattern lengths that were used in the phantom
study. Notably, all patterns feature slowly varying flip angles, indicating
that smooth signal shapes may increase the robustness to undersampling
artifacts. The resulting mean RMSEs for T1 and T2 in the
tubes are shown in Fig. 2a and b. The overall errors were found to decrease with
increasing pattern length until L=500. Further increasing the pattern lengths
to L=1000 and more did not lead to a substantial reduction of the T1
and T2 errors, independent of the employed acceleration factor. Consequently,
the maximum efficiency of the employed FA patterns, as shown in Fig. 2c and d, decreased
for L>500. The highest overall efficiency was achieved with L=500 (i.e., the
pattern in Fig. 1c) and R=30.Conclusion
The presented approach allows to find the most efficient MRF sequence for a desired level of accuracy. With our setup, a sequence length of L=500 showed the highest overall efficiency. Since the signal-dependent noise that was employed in this study represents an approximation of the artifacts due to undersampling, the presented optimized FA patterns cannot be expected to be suitable for recently proposed approaches for improved reconstruction of the MRF image series5. Future work will include sequence optimization for these cases and a validation of the presented findings in vivo.Acknowledgements
No acknowledgement found.References
[1] Ma D et al., Nature 2013;495:187-192 [2] Sommer K et al., Proc ISMRM 2016; #429 [3] Jiang Y et al., Magn Res Med 2015;74(6):1621-31[4] Deoni et al., Magn Res Med 2003;49(3):515-26 [5] Zhao B et al., Proc ISMRM 2016; #871
Figures
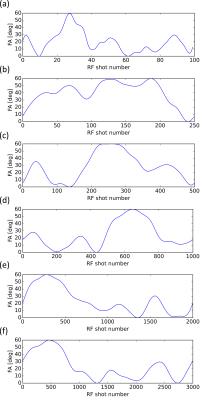
Fig. 1: The optimized FA patterns for the six different pattern
lengths that were employed in the phantom study.
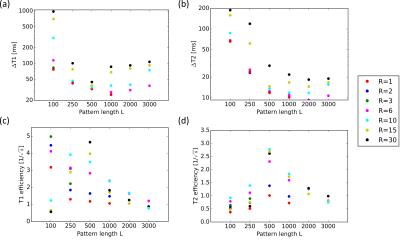
Fig. 2: The mean RMSEs in the tubes for T1 (a) and
T2 (b) as well as the calculated efficiencies for T1 (c)
and T2 (d) for the six different pattern lengths as well as for
different acceleration factors. Acceleration factors lower than R=6 were not
employed for the two longest pattern lengths (L=2000 and L=3000). Note that
both (a) and (b) are shown in logarithmic scale.