1465
Fast Bloch-Torrey simulation of 3D RF spoiled gradient echo sequences using a number of subvoxels and molecular diffusion effectRyoichi Kose1 and Katsumi Kose2
1MRTechnolocy, Inc., Tsukuba, Japan, 2University of Tsukuba, Tsukuba, Japan
Synopsis
RF spoiled gradient echo sequences were studied both with experiments and Bloch-Torrey simulation. The Bloch simulation of the 256×256×32 voxel images clarified that adequate number of subvoxels were required for artifact-free images. The Bloch-Torrey simulation for one voxel magnetization clarified that adequate number of subvoxels were required for image intensity reproduction by diffusion effect. In conclusion, molecular diffusion effects are indispensable to reproduce the image contrast in SPGR.
Introduction
RF spoiled gradient echo sequences (SPGR) are widely used for fast T1 weighted imaging and fast T1 mapping [1,2]. The SPGR sequences are quite attractive from a viewpoint of computer simulation of the imaging process because the coherence of the nuclear magnetization is apparently broken between TRs but has an important role for the image contrast. In this study, we performed fast Bloch-Torrey simulation and experiments for the SPGR sequences and demonstrated the importance of the molecular diffusion for the image contrast.Materials and Methods
We used a home built 1.5 T MRI system consisting of a horizontal bore (280 mm) superconducting magnet, a second-order shim coil, an insertable gradient coil set, a transmit-receive birdcage coil, and a digital MRI console (MRTechnology, Tsukuba, Japan). A cylindrical phantom consisting of three small cylindrical PET bottles stored in an acrylic container filled with baby oil was used. The PET bottles were filled with CuSO4 water solution with different densities, whose T1 (~T2) were about 114, 244, and 351 ms, respectively. The cylindrical phantom was imaged with 3D SPGR sequences (TR/TE = 20ms/6ms, FA = 30°, image matrix = 256×256×32, bandwidth = 50 kHz, FOV = (64 mm)3). The RF pulse phase φ was changed as φ=n(n + 1)Φ/2, where n is the number of the RF pulse in the SPGR sequence and Φ (phase shift base angle) was changed from 0 to 359 degree by one degree step. The SPGR sequences were simulated using the Bloch equation for 256×256×32 voxel images and simulated using the Bloch-Torrey equation for one voxel magnetization. The number of subvoxels was 1-129 for the Bloch equation and 8-128 for the Bloch-Torrey equation. The effect of the isotropic molecular diffusion was calculated using the second order spatial derivative of the nuclear magnetization along the readout direction. The Bloch simulation was performed using a GPU optimized MRI simulator [3] with two GPU boards (GeForce GTX1080).Results
Figure 1 shows cross-sections selected from 3D image datasets calculated using the SPGR sequence (Φ = 117°) when the number of subvoxel was changed. Considerable stripe artifacts were observed when the number of subvoxels was small but disappeared when it exceeded 65. Figure 2 shows cross-sections selected from 3D image datasets (a) experimentally acquired and (b) calculated with 65 subvoxels. The image contrast at Φ=117° was nearly identical between the experiment and the simulation but that at Φ=120° and 180° was different. Figure 3 shows image intensity of each part of the cylindrical phantom acquired with the SPGR sequences plotted against Φ. While the image intensity measured for the calculated image datasets shown in Fig.3(b) showed many distinct peaks, that measured for the acquired image datasets shown in Fig.3(a) showed only a few small peaks except that of the baby oil. Figure 4 shows molecular diffusion effects calculated for one voxel using the Bloch-Torrey equation. Figure 4(a) shows image intensity of the CuSO4 doped water (T1 = T2 = 351 ms, D = 0.00316 mm2/s (water at 35°C)) calculated for the SPGR sequences when the number of subvoxels was changed. While the peak height decreased with the increased number of subvoxels, the shapes of the peaks with 64 and 128 subvoxels were identical. Figure 4(b) shows image intensity of the doped water calculated for the SPGR sequences with 64 subvoxels when the diffusion constant was changed. This graph clearly demonstrates that the peak height decreased with the increase of the diffusion constant. Figure 5 shows signal intensity of each part of the cylindrical phantom calculated for the SPGR sequences (a) without (b) and with the molecular diffusion effect using the Bloch-Torrey equation. These graphs clearly demonstrate that the experimental results for the SPGR sequences were reproduced by the diffusion effect.Discussion
The result that more than 65 subvoxels were required to describe the motion of the nuclear magnetization in the SPGR sequences as shown in Fig.1 demonstrates the presence of the transverse coherence over a few tens of TR periods as suggested by the EPG theory [4]. The result that more than 64 subvoxels were required to describe the molecular diffusion effect as shown in Fig.4(a) is caused by the same mechanism. In conclusion, the image contrast in the SPGR sequences can be reproduced by the Bloch-Torrey simulation with adequate number of subvoxels determined by the coherent length of the nuclear magnetization.Acknowledgements
This work is supported by Japan Science and Technology Agency.References
[1] Zur Y, Wood ML, Neuringer LJ. Spoiling of transverse magnetization in steady-state sequences. Magn Reson Med 1991;21:251–263. [2] Fram EK, Herfkens RJ, Johnson GA, Glover GH, Karis JP, Shimakawa A, Perkins TG, Pelc NJ. Rapid calculation of T1 using variable flip angle gradient refocused imaging. Magn Reson Imaging 1987;5: 201–208. [3] Kose R, Kose K, GPU optimized fast 3D MRI simulator, Proc. Intl. Soc. Mag. Reson. Med. 24 (2016) 3202. [4] Weigel M, Extended phase graphs: dephasing, RF pulses, and echoes - pure and simple, J Magn Reson Imaging. 2015; 41(2): 266-95.Figures
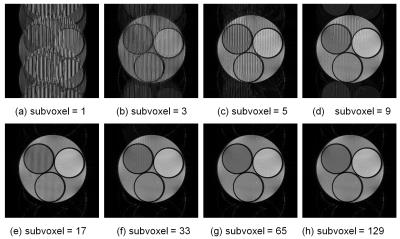
Cross-sectional images selected from 3D image datasets of a numerical
phantom simulated for the RF spoiled gradient echo sequence (TR/TE = 20ms/6ms,
FA = 30°,
image matrix = 256×256×32) using various number of subvoxels.
When the number of subvoxel is larger than 65, the stripe artifacts cannot be
seen. T1 and T2 of the CuSO4 water solution in
the small bottles were 114, 244, 351 ms and those of the baby oil surrounding
the bottles were 186 and 80 ms. The resonance frequency difference between the
water and the oil was 220 Hz in the simulation.
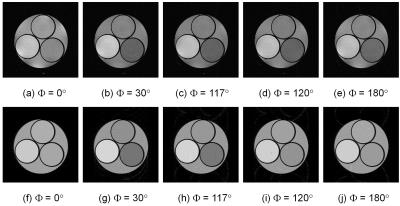
Cross-sectional
images selected from 3D image datasets acquired with the SPGR sequences (TR/TE
= 20ms/6ms, FA = 30°,
image matrix = 256×256×32, FOV
= (64 mm)3). Φ is phase shift base angle described in the text.
(a)-(e): Acquired with the experiments at 1.5 T. (f)-(j) Acquired with the Bloch
simulation (without diffusion effect). The number of subvoxel is 65. The processing speed was about 8 TFLOPS. The actual
size of the cylindrical phantom: diameter = 45 mm, length = 60 mm, diameter of
the small bottles = 20 mm. The relaxation times are described in the caption of
Fig.1.
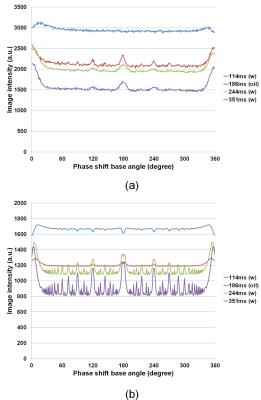
Image intensity of each part of the cylindrical phantom acquired with
the SPGR sequences plotted against Φ. The
phase of the RF pulse was varied as n(n+1)Φ/2, where n is the RF pulse
number. (a) Acquired with a 1.5 T MRI system. (b) Simulated with the number of
subvoxels = 65. The blue, green, and violet lines correspond to CuSO4
solution with T1 and T2 of 114, 244, and 351 ms. The
brown lines correspond to baby oil with T1 = 186 ms and T2
= 80 ms.
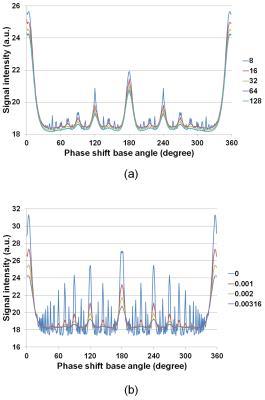
Molecular diffusion effects calculated for one voxel magnatization using
the Bloch-Torrey equation. (a) Image intensity of the CuSO4 doped
water (T1 = T2 = 351 ms, D = 0.00316 mm2/s
(water at 35°C)) calculated
for the SPGR sequences when the number of subvoxels was 8, 16, 32, 64, and 128.
(b) Image intensity of the doped water calculated for the SPGR sequences with
64 subvoxels when the isotropic diffusion constant was 0, 0.001, 0.002, and
0.00316 mm2/s.
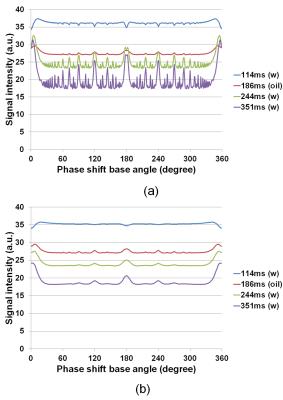
Signal
intensity of each part of the cylindrical phantom calculated for the SPGR
sequences using the Bloch-Torrey equation. (a) Without the molecular diffusion
effect. (b) With the molecular diffusion effect