1460

Obtaining accurate and fast unwrapped phase images

Riccardo Metere¹ and Harald E. Möller¹

¹NMR Unit, Max Planck Institute for Human Cognitive and Brain Sciences, Leipzig, Germany

Synopsis

The unwrapping of phase data is a common problem in MRI. However, its solution is non-trivial for 2D or 3D images, and there has been some general research in this direction, notably in the field of optics. The two most pupular algorithms for MRI applications are: (i) a Laplacian-based method that is fast but inaccurate; (ii) a region-merging optimization method that is accurate but very slow. Here, we propose the adoption of a recently developed and freely available unwrap algorithm that significantly outperforms the other considered methods, allowing for both fast and accurate calculation of unwrapped phase images.

Purpose

The analysis of MRI data has been traditionally linked to the interpretation of the magnitude of the complex signals obtained from the receive coil, because of its relative insensitivity to undesired experimental conditions. In recent years there has been a growing interest in the extraction of information from the phase of such complex signals for obtaining additional information on the sample, e.g. in susceptibility imaging¹, in relaxometry², in diffusion imaging³. Because of the nature of complex numbers, the phase images are defined within the $$$[-\pi,\pi)$$$ range. Therefore, the resulting images are often characterized by a number of discontinuities in regions where the phase variation is larger than $$$2\pi$$$. In many applications, "continuous" functions are often desired, and an unwrapping step is often necessary. However, the problem of unwrapping is non-trivial in N-dimensions for $$$N > 1$$$, and many algorithms have been proposed and implemented in the major software packages for MRI analysis. Here, we investigate the accuracy and speed of such algorithms for the unwrapping of typical MRI data.

Methods

Full brain 3D-FLASH images were acquired (using MAGNETOM Siemens scanners):

Verio 3T

- $$$T_R=30\;\mathrm{ms}$$$, $$$T_E=17\;\mathrm{ms}$$$, $$$\alpha=13\mathrm{°}$$$, $$$0.8\;\mathrm{mm}$$$ isotropic resolution; matrix size: $$$208\mathrm{x}256\mathrm{x}160$$$

- Tx: body coil, Rx: 32-channel head coil;

- 1 healthy volunteer (female, age: 30).

- $$$T_R=29\;\mathrm{ms}$$$, $$$T_E=18.35\;\mathrm{ms}$$$, $$$\alpha=11.23\mathrm{°}$$$, $$$0.6\;\mathrm{mm}$$$ isotropic resolution; matrix size: $$$260\mathrm{x}320\mathrm{x}256$$$

- circularly polarized Tx / 32-channel Rx head coil;

- 1 healthy volunteer (female, age: 25).

Three unwrapping algorithms were tested:

1. The Laplacian-based method⁴, as implemented by the PyMRT Python package (giving identical results to the MATLAB implementation by the Nottingham group);

2. The region-mergin optimization method⁵ as implemented by FSL 5.0⁶;

3. The sorting-path method^7,8 as implemented in the scikit.image Python package (a command-line interface to that is provided in PyMRT).

Computation times for the different unwrapping solutions are reported for calculation with a workstation equipped with an Intel® Core™ i7-3770K CPU @3.50GHz quad-core processor and 16 GB of memory. The accuracy of the unwrapping was evaluated by calculating the difference between the unwrapped and the wrapped images, and the normalized mutual information coefficient $$$nMI$$$, with low signal-to-noise ratio (SNR) voxels excluded from the computations, because the phase information is not well defined there.

Results

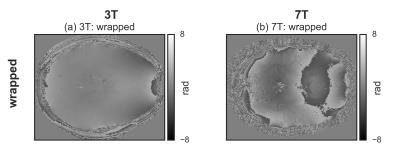
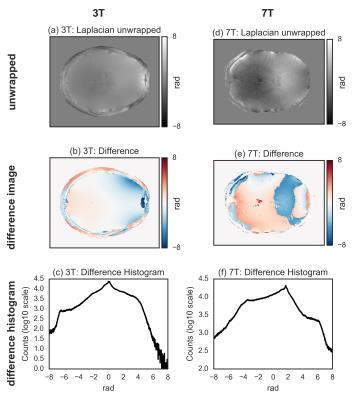
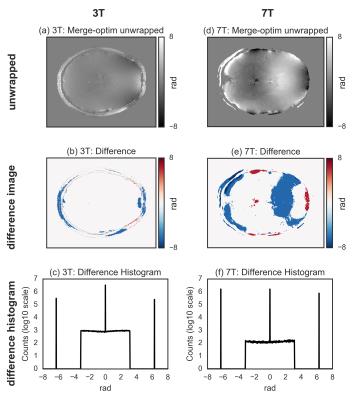
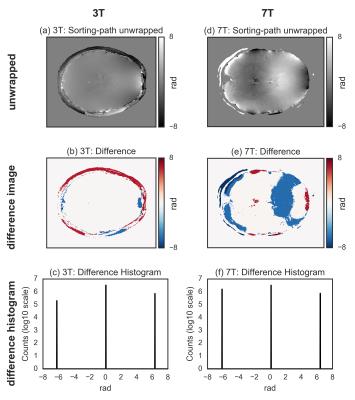
For both 3T and 7T data, the wrapped image (Fig.[1]), the difference with the unwrapped image, and the histogram of the difference, for the three tested methods are shown in Fig.[2],[3],[4]. The region-merging optimization and the sorting-path methods are remarkably accurate, as evident from the very flat appearance of the difference images, and its corresponding histograms, where extremely sharp peaks (separated by $$$2\pi$$$ multiples) are observed. On the contrary, the Laplacian-based method is relatively inaccurate, as evidenced by the difference images and the corresponding histograms, where the expected $$$2\pi$$$ peaks are too broad to be resolved.

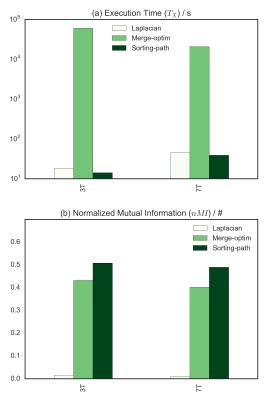
A summary of the algorithms performance (both $$$nMI$$$ and execution time $$$T_X$$$) for all implementations is presented in Fig.[5]. The region-merging optimization algorithm execution time is remarkably longer compared to the other two, the sorting-path method being the fastest with the tested implementation).

Discussion

The difference image cannot be used for direct quantification of the accuracy because the phase is defined up to an arbitrary constant offset. However, the difference between the unwrapped and the wrapped images should only contain values that are multiple of $$$2\pi$$$. Deviations from this behavior is reflected relatively well by the degradation (decrease) of the normalized mutual information coefficient.

Additionally, the Laplacian operator is implemented in the Fourier domain and is relatively sensitive to the parameters affecting the numerical values of the discrete Fourier transform, notably the matrix size. In particular we observed a different bias introduced in the Laplacian-based unwrapping when investigating the effect of the matrix size on the final results. However, they were all qualitatively similar, and the accuracy improved only marginally for larger matrix sizes. Regarding the speed of the Laplacian-based method, the tested implementation rely on the efficiency of the Fourier transform, and other implementations might be faster.

Note that the Laplacian operator is also used in other MRI applications, notably quantitative susceptibility mapping (QSM), which may be relatively robust against to (possibly only the low frequency components of) the bias introduced in the unwrapped images by the Laplacian-based unwrapping method. This aspect remains to be investigated.

Conclusion

The phase unwrapping method based on sorting by reliability following a non-continuos path performs significantly better in terms of accuracy respect to the tested Laplacian-based implementations.

Acknowledgements

We would like to thank the following people: Andreas Schäfer, Pierre-Louis Bazin, Tobias Leutritz and Kerrin Pine for helpful discussions; Ahmad S. Kanaan, Christopher Steele, Christine Tardif and Claudine Gauthier for kindly sharing data; Richard Bowtell for sharing portions of code. Funded by: EU through the 'HiMR' Marie Curie ITN (FP7-PEOPLE-2012-ITN-316716), the Max Planck Society through IMPRS NeuroCom, and the Helmholtz Alliance 'ICEMED'.

References

1. Schäfer, A., Wharton, S., Gowland, P., Bowtell, R., 2009. Using magnetic field simulation to study susceptibility-related phase contrast in gradient echo MRI. NeuroImage 48, 126–137. doi:10.1016/j.neuroimage.2009.05.093

2. Labadie, C., Lee, J.-H., Rooney, W.D., Jarchow, S., Aubert-Frécon, M., Springer, C.S., Möller, H.E., 2014. Myelin water mapping by spatially regularized longitudinal relaxographic imaging at high magnetic fields. Magn. Reson. Med. 71, 375–387. doi:10.1002/mrm.24670

3. Eichner, C., Cauley, S.F., Cohen-Adad, J., Möller, H.E., Turner, R., Setsompop, K., Wald, L.L., 2015. Real diffusion-weighted MRI enabling true signal averaging and increased diffusion contrast. NeuroImage 122, 373–384. doi:10.1016/j.neuroimage.2015.07.074

4. Schofield, Marvin A., and Yimei Zhu. “Fast Phase Unwrapping Algorithm for Interferometric Applications.” Optics Letters 28, no. 14 (July 15, 2003): 1194–96. doi:10.1364/OL.28.001194.

5. Jenkinson, M., 2003. Fast, automated, N-dimensional phase-unwrapping algorithm. Magn. Reson. Med. 49, 193–197. doi:10.1002/mrm.10354

6. Jenkinson, M., Beckmann, C.F., Behrens, T.E.J., Woolrich, M.W., Smith, S.M., 2012. FSL. NeuroImage, 20 YEARS OF fMRI 62, 782–790. doi:10.1016/j.neuroimage.2011.09.015

7. Herráez, M.A., Burton, D.R., Lalor, M.J., Gdeisat, M.A., 2002. Fast two-dimensional phase-unwrapping algorithm based on sorting by reliability following a noncontinuous path. Applied Optics 41, 7437. doi:10.1364/AO.41.007437

8. Abdul-Rahman, H., Gdeisat, M., Burton, D., Lalor, M., 2005. Fast three-dimensional phase-unwrapping algorithm based on sorting by reliability following a non-continuous path. pp. 32–40. doi:10.1117/12.611415

9. Uecker, M., Lai, P., Murphy, M.J., Virtue, P., Elad, M., Pauly, J.M., Vasanawala, S.S., Lustig, M., 2014. ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA. Magn. Reson. Med. 71, 990–1001. doi:10.1002/mrm.24751

10. Uecker, M., Lustig, M., 2016. Estimating absolute-phase maps using ESPIRiT and virtual conjugate coils. Magn. Reson. Med. doi:10.1002/mrm.26191

11. Bilgic, B., Polimeni, J.R., Wald, L.L., Setsompop, K., 2015. Automated tissue phase and QSM estimation from multichannel data, in: #2849. Presented at the ISMRM 23rd Annual Meeting & Exhibition, Toronto, Canada.

Figures

Fig.1: The input phase for the (a) 3T and (b) 7T data. Note the presence of more pronounced wrapping in the original phase for the 7T data, which reflects the current status of the typical homogeneity of the main magnetic field achievable with 3T and 7T scanners. The data for each coil was recombined using ESPIRiT and a recently proposed singular value decomposition (SVD)-based method for estimating the virtual coil reference from the same data^9,10,11.

Fig.2: Evaluation of the Laplacian-based unwrapping method. The columns refer to 3T and 7T data, respectively. The (masked) unwrapped image is shown (first row) along with the difference with the wrapped phase image (second row) and the histogram of the difference image (third row). Note the presence of non-constant offsets between the wrapped and the unwrapped images.

Fig.3: Evaluation of the region-merging optimization unwrapping method. The columns refer to 3T and 7T data, respectively. The (masked) unwrapped image is shown (first row) along with the difference with the wrapped phase image (second row) and the histogram of the difference image (third row). Results are mostly as expected for accurate unwrapping.

Fig.4: Evaluation of the sorting-path unwrapping method. The columns refer to 3T and 7T data, respectively. The (masked) unwrapped image is shown (first row) along with the difference with the wrapped phase image (second row) and the histogram of the difference image (third row). Results are entirely as expected for accurate unwrapping.

Fig.5: Evaluation of the performances of the unwrapping methods. The speed performances are reported in terms of execution time $$$T_X$$$ of a single run on a dedicated workstation (first row), while the accuracy is estimated from the normalized mutual information ($$$nMI$$$) between the unwrapped and the wrapped images (second row). Note that the execution time scale is logarithmic. The sorting-path algorithms outperforms the other algorithms both for accuracy and speed (with the current implementation). The time required for the region-merging optimization algorithm can be reduced by excluding larger portions of data with low SNR.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)

1460