1457
Optimization of multiple orientation QSM for building a clinically feasible protocol1Center for Neuroscience and Regenerative Medicine, National Institute of Helath, Bethesda, MD, United States
Synopsis
Quantitative Susceptibility Mapping (QSM) offers unique, quantitative information about tissue magnetic susceptibility. A multi-orientation method, calculation of susceptibility through multi-orientation sampling (COSMOS), enables the dipole inversion by acquiring data at multiple orientations. In practical imaging settings, however, it is a challenge to image the subject multiple orientations. Although small angle COSMOS has been shown to generate reasonable QSM images, the selection of orientations within a practical acquisition protocol remains an open question. In this work, we investigated the influence of the number and direction of orientations on the outcome of small angle COSMOS for in vivo imaging.
Introduction
Quantitative Susceptibility Mapping (QSM) offers unique, quantitative information about tissue magnetic susceptibility. A major challenge in QSM is inverting the acquired phase measurement to estimate the underlying susceptibility. The inversion is ill-posed because the dipole kernel in k-space is zero on the cone surface at polar angles of ±54.7° with respect to B0(1). A multi-orientation method, calculation of susceptibility through multi-orientation sampling (COSMOS), enables the dipole inversion by acquiring data at multiple orientations (≥3) to transform the problem into an over-determined linear system. It has been shown to provide better estimates than regularized QSM from a single orientation(2) . In practical imaging settings, however, it is a challenge to image the subject at orientations with optimal angles that are evenly distributed over π. Although small angle COSMOS with 2 and 3 orientations has been previously used to generate QSM mappings (3), the selection of orientations within a practical acquisition protocol remains an open question. In this work, we investigated the influence of the number and direction of orientations on the outcome of small angle COSMOS for in vivo imaging. We employ an accelerated susceptibility weighted imaging acquisition with an open head coil configuration that could potentially be routinely applied for clinical use.Materials and Methods
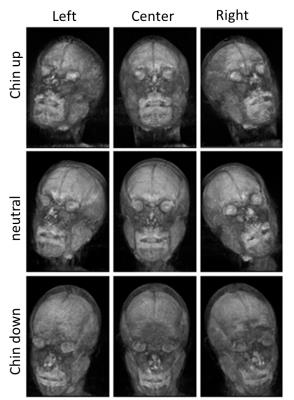
MRI acquisition: A healthy volunteer was scanned on a 3.0 T Biograph mMR (Siemens, release VB20P) after informed consent under an IRB approved protocol. To provide room to acquire whole head images using different head orientations, a relatively spacious arch shaped support (34 cm in diameter) was built to allow two six element flexible coil arrays (Siemens mMR body TIM) to be used for imaging. SWI from nine head orientations combining 3 flexion/extension (neutral, chin-up, chin-down) orientations with 3 rotation (right, center, left) was acquired using sagittal 3D segmented EPI (2m21s acquisition time) aligned to the gantry axes.. Parameters were: FOV=256×176×256, voxel size =1 mm3, TE/TR/FA=25ms/64ms/12°, ETL=15. The scan time for each orientation was 2 minutes 21 seconds QSM processing: Susceptibility was computed as follows: (1) Laplacian-based phase unwrapping (4), (2) SHARP filtering with a varying spherical kernel (5), (3) FLIRT (6) registration of magnitude images for each head position to neutral applied to the tissue phase data, and (4) deconvolution using the regularized COSMOS (regularization parameter λ=0.006) algorithm (7). For comparison purposes, susceptibility was also estimated from each single orientation using thresholded k-space division (TKD) (3).
Data analysis: All possible combinations of the 9 orientations were used to generate QSM maps. The number of orientations used at a time ranged from 2 to 8 orientations. For example, a selection of 2 orientations from 9 orientations would result in 36 combinations. Then for each orientation set a combination was selected that would result in the lowest mean squared error relative to a reference QSM map computed from all 9 orientations.
Results
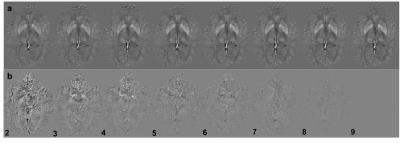
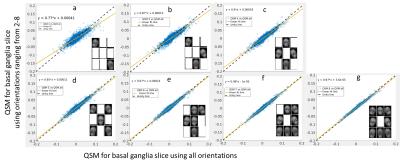
Figure 2a shows QSM maps of a slice containing basal ganglia generated using different number of head orientations and Figure 2b shows the difference maps of difference map generated from these maps subtracted with reference. Figure 3 (a-g) shows scatter plots of QSM maps generated using multiple orientations to visualize the deviation of QSM maps relative to the reference. A linear line was fit to the data to estimate the slope. The optimal orientation combination is shown in the bottom right of each plot. As expected, the variation of the susceptibilities from reference decreases with increasing number orientations and the slope of the linear fit converges to unity. Figure 4 shows the plot of slope of the fitted line with the number orientations.
Discussion and Conclusion
In this study we observed that regularized COSMOS with relatively fewer orientations can be used to estimate susceptibility with minimal streaking artifacts. Although fewer orientations results in some loss of accuracy, the scan protocol can be adjusted with respect to amount of accuracy required for a particular application. The slope error in two orientation COSMOS (23%) was lower than the TKD (30%). Using four orientations achieves a slope error of only 5% and can be acquired in less than 10 minutes. Thus, in combination with the accelerated imaging sequence using segmented EPI, minimizing the number of head orientations required to generate the QSM could potentially lead to lower patient discomfort and faster adaptation into clinical settings.Acknowledgements
This work was supported by Center for Neuroscience and Regenerative Medicine (CNRM) and the intramural Program of the National Institutes of Health.References
1. Wang Y, Liu T. Quantitative susceptibility mapping (QSM): Decoding MRI data for a tissue magnetic biomarker. Magnetic resonance in medicine : official journal of the Society of Magnetic Resonance in Medicine / Society of Magnetic Resonance in Medicine 2015;73:82-101.
2. Liu T, Spincemaille P, de Rochefort L, Kressler B, Wang Y. Calculation of susceptibility through multiple orientation sampling (COSMOS): a method for conditioning the inverse problem from measured magnetic field map to susceptibility source image in MRI. Magnetic resonance in medicine : official journal of the Society of Magnetic Resonance in Medicine / Society of Magnetic Resonance in Medicine 2009;61:196-204.
3. Wharton S, Schäfer A, Bowtell R. Susceptibility mapping in the human brain using threshold-based k-space division. Magnetic resonance in medicine 2010;63:1292-1304.
4. Li W, Avram AV, Wu B, Xiao X, Liu C. Integrated Laplacian-based phase unwrapping and background phase removal for quantitative susceptibility mapping. NMR in biomedicine 2014;27:219-227. 5. Schweser F, Deistung A, Lehr BW, Reichenbach JR. Quantitative imaging of intrinsic magnetic tissue properties using MRI signal phase: an approach to in vivo brain iron metabolism? NeuroImage 2011;54:2789-2807. 6. Jenkinson M, Smith S. A global optimisation method for robust affine registration of brain images. Medical image analysis 2001;5:143-156.
7. Bilgic B, Xie L, Dibb R, Langkammer C, Mutluay A, Ye H, Polimeni JR, Augustinack J, Liu C, Wald LL, Setsompop K. Rapid multi-orientation quantitative susceptibility mapping. NeuroImage 2016;125:1131-1141.
Figures