1445
Bias and SNR of $$$T_1$$$ estimates derived from joint fitting of actual flip-angle and FLASH imaging data with variable flip angles1Radiology, Perelman School of Medicine, University of Pennsylvania, Philadelphia, PA, United States
Synopsis
Previous work has suggested fitting joint AFI/FLASH data for T1 and B1+ by minimizing the 2-norm of the difference between the signal model and measurements will produce unbiased estimates of T1. We demonstrate that, contrary to previous results, the estimator has a substantial bias that varies with both the true T1 and B1+, and the receive channel count. We also demonstrate that the correct ML estimator removes the effect of channel count, and that the choice of AFI protocol has a larger impact of the quality of estimates than the addition of an extra FLASH scan.
Introduction
The use of actual flip-angle imaging (AFI) [1], combined with multiple FLASH scans acquired at a range of flip angles has been well-studied as a method for efficient $$$T_1$$$ mapping [2-9], simultaneously accounting for error in $$$B_1^+$$$. Most previous work has first fit the AFI to estimate $$$B_1^+$$$, then used this map in fitting the FLASH data. More recent work has claimed that jointly fitting all the data by minimizing the 2-norm between the signal model and the measured magnitudes would produce unbiased estimates of $$$T_1$$$ [9]. Contradicting this, in the present work we show that fitting this model with realistic noise actually produces highly biased estimates, even when assuming the signal model is perfect (e.g., perfect spoiling, etc.). We additionally show that fitting the correct maximum likelihood estimator (MLE), previously shown to be computationally efficient [10], produces substantially less-biased estimates of $$$T_1$$$ from the same data.
Methods
Signals were generated from the standard AFI signal model equation for two AFI protocols, both with 55~degree flip angles, but one having TRs of 30 ms and 150 ms (long-AFI) while the second had TRs of 10 ms and 50 ms (short-AFI). We also generated signals for two FLASH scans, both with TR 10 ms, but flip angles 3~degrees and 18~degrees. Protocols were matched to [9]. T1 values from 100 ms to 2000 ms were simulated in 50 ms increments, while values of the flip angle error $$$\epsilon$$$ were varied from 0.5 to 1.5 in increments of 0.05. From these signal models four possible "experiments" were simulated: long-AFI or short-AFI with just the 3-degree FLASH scan, and long-AFI or short-AFI with both FLASH scans. For each of the experiments, at each of the $$$T_1$$$ and $$$\epsilon$$$ values, we simulated $$$10^4$$$ measurements. For each measurement, sensitivities for 1-, 12-, 32-, and 64-channel receive coils were simulated by randomly drawing points from a uniform distribution on the unit $$$2n$$$-dimensional sphere for each simulated sample where $$$n$$$ is the number of simulated channels, and treating the resulting $$$2n$$$ values a complex $$$n$$$-vector. Drawing new coil sensitivity models for each simulation captures this additional source of variation in real data. Constraining sensitivites to the unit sphere ensures that, in the case of perfect knowledge of the coils' sensitivities, the number of channels does not affect the SNR of the channel-combined signal. Additionally, we chose three scale factors of 500, 1000, and 2000, roughly representing a range of baseline proton density based on empirical observations of SNR from our own scanners. After multiplying the signal model by the scale factor and the current coil sensitivity, independent samples of unit-variance circular complex Gaussian noise were added to each channel. Each sample was fit with both the MLE [10], and also with a model that minimized the 2-norm difference between the signal model and the RMS of the channels [9]. The $$$10^4$$$ estimates in each condition were used to compute bias and variance for each estimator.Results
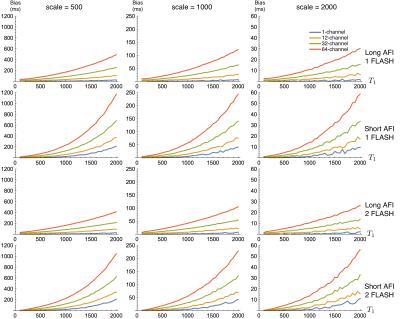
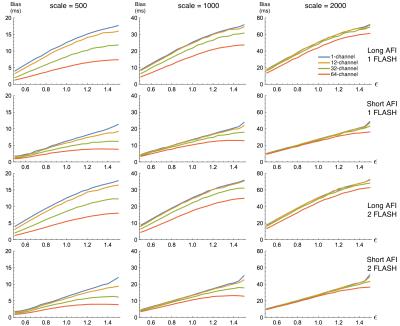
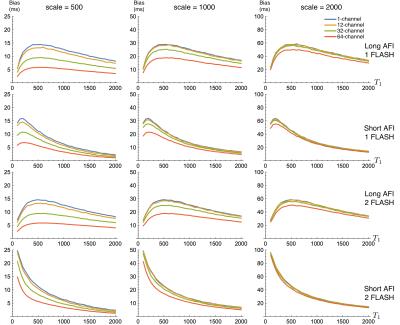
In all SNR/signal conditions the MLE estimator for all channel-counts produced effectively the same bias and variance estimates as the 1-channel RMS estimator (difference on same scale as Monte Carlo estimation noise). Thus, for the purposes of plotting we show only the RMS results. Bias across $$$\epsilon$$$ and $$$T_1$$$ are plotted in Figures 1 and 2, respectively. $$$SNR_{T_1} = T_1/\sqrt(bias^2 + variance)$$$ across $$$\epsilon$$$ and $$$T_1$$$ are is plotted in Figures 3 and 4.Discussion
Our results clearly show a significant bias in estimation of $$$T_1$$$, regardless of estimator used, that depends on both true $$$T_1$$$ and $$$\epsilon$$$. For the previously-described RMS-based estimator, this bias also varies with channel count; an effect that is removed by using the correct MLE for the data. Our results on bias differ from those in previous work claiming an unbiased estimator because we have used the correct noise model in our Monte Carlo simulation.
We also note that the addition of a second FLASH scan seems to add little improvement to $$$T_1$$$ estimation, while the choice of AFI protocol appears to have a large impact.
Conclusions
We have demonstrated that the MLE, accounting for the noise in multi-channel data, produces substantially lower bias and higher $$$T_1$$$-SNR than previously proposed estimation algorithms for joint AFI/FLASH data using multi-channel coils. Our results support the proposal of estimating $$$T_1$$$ from all the measurements jointly, but also demonstrate the need to carefully model noise properties when performing Monte Carlo simulations of quantiative models in MRI. Given the correct noise model, we have shown that the previously described $$$T_1$$$ estimator is not unbiased.
Acknowledgements
This work was funded by NICHD R00HD074649.References
1. Yarnykh, Vasily L. "Actual flip-angle imaging in the pulsed steady state: a method for rapid three-dimensional mapping of the transmitted radiofrequency field." Magnetic resonance in Medicine 57, no. 1 (2007): 192-200.
2. Gupta, Raj K. "A new look at the method of variable nutation angle for the measurement of spin-lattice relaxation times using fourier transform NMR." Journal of Magnetic Resonance (1969) 25, no. 1 (1977): 231-235.
3. Wang, Henry Z., Stephen J. Riederer, and James N. Lee. "Optimizing the precision in T1 relaxation estimation using limited flip angles." Magnetic Resonance in Medicine 5, no. 5 (1987): 399-416.
4. Deoni, Sean CL, Terry M. Peters, and Brian K. Rutt. "Determination of optimal angles for variable nutation proton magnetic spin-lattice, T1, and spin-spin, T2, relaxation times measurement." Magnetic resonance in medicine 51, no. 1 (2004): 194-199.
5. Sijbers, Jan, Arnold Jan den Dekker, Erik Raman, and Dirk Van Dyck. "Parameter estimation from magnitude MR images." International Journal of imaging systems and technology 10, no. 2 (1999): 109-114.
6. Fischl, Bruce, David H. Salat, André JW van der Kouwe, Nikos Makris, Florent Ségonne, Brian T. Quinn, and Anders M. Dale. "Sequence-independent segmentation of magnetic resonance images." Neuroimage 23 (2004): S69-S84.
7. Chang, Lin-Ching, Cheng Guan Koay, Peter J. Basser, and Carlo Pierpaoli. "Linear least-squares method for unbiased estimation of T1 from SPGR signals." Magnetic resonance in medicine 60, no. 2 (2008): 496-501.
8. Trzasko, Joshua D., Petrice M. Mostardi, Stephen J. Riederer, and Armando Manduca. "Estimating T1 from multichannel variable flip angle SPGR sequences." Magnetic resonance in medicine 69, no. 6 (2013): 1787-1794.
9. Hurley, Samuel A., Vasily L. Yarnykh, Kevin M. Johnson, Aaron S. Field, Andrew L. Alexander, and Alexey A. Samsonov. "Simultaneous variable flip angle–actual flip angle imaging method for improved accuracy and precision of three-dimensional T1 and B1 measurements." Magnetic resonance in medicine 68, no. 1 (2012): 54-64.
10. Tisdall, M. Dylan, and van der Kouwe, Andre J. W. "Efficient maximum likelihood estimation of T1, T2∗, and flip angle error using variable-length echo trains in combined AFI and FLASH experiments." Proceedings of the ISMRM 2015.
Figures