1441
Fast fitting method for simultaneously quantifying multiple MR parameters using local optimization method with predetermined initial values1Research & Development Group, Hitachi, Ltd., Tokyo, Japan
Synopsis
A fast fitting method for quantifying multiple MR parameters using local optimization method with predetermined initial values is proposed. In the proposed method, an optimal neighborhood solution is extracted as predetermined initial values. A difference in MR parameters between the proposed method and the conventional method was less than 5 %. On the other hand, a computing time of the proposed method was approximately 15 times faster compared with the conventional method. We concluded that the proposed method can provide fast fitting process while maintaining calculation accuracy.
Purpose
Quantitative MR parameters are expected to improve multi-center studies and reduce inter-reader variability1. Previously, we have developed a technique for simultaneously quantifying multiple MR parameters (T1, T2*, PD and B1) by fitting a signal equation to RF-spoiled gradient echo images obtained with various scan parameters2. In the developed method, an interpolation function obtained from discrete data calculated by the Bloch simulation is used as the signal equation. In the fitting process, a global optimization method (such as simulated annealing method) is conventionally used to avoid convergence on a local solution. However, the process is time consuming due to increase in the number of repetitive calculation. To address the problem, we propose a fast fitting method for quantifying multiple MR parameters using local optimization method with predetermined initial values.Method
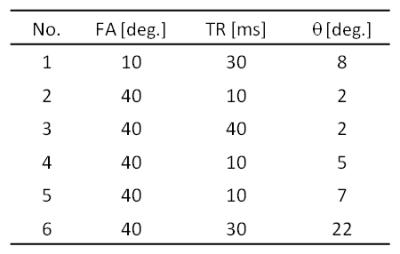
Three-dimensional RF-spoiled gradient echo sequence was performed on a healthy volunteer using a 3 T MRI system (Hitachi, Ltd., Japan) and a 32-channel head coil. Six images were obtained with different scan parameters, which are as shown in Table 1. Other parameters were as follows: TE, 4.6 ms; matrix, 148×186×148; resolution, 1.1×1.1×1.1 mm3; and acquisition time, 14 min 37 s.
In this study, the signal intensity of RF-spoiled gradient echo, S, is described with the following equation2.
$$S=PD^{*}\times f(T1, T2, B1\times FA, TR, \theta) (1),$$
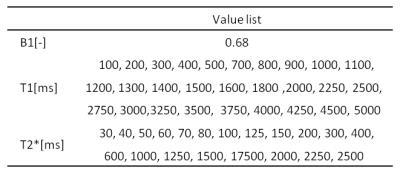
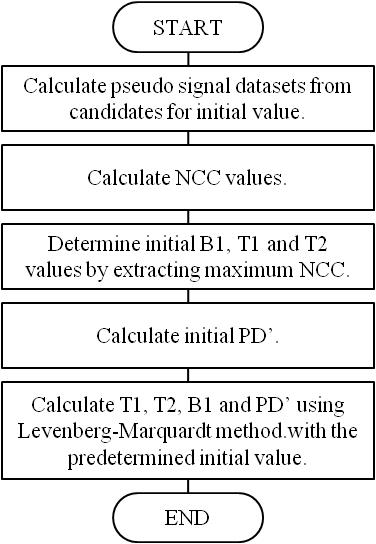
where, TR is repetition time, FA is flip angle, θ is phase cycling of RF, PD’ is proton density × coil sensitivity. The function f was formulated numerically by cubic polynomial interpolation of the total of 217,350 signal intensity datasets, which were calculated by using the Bloch simulation3 with different combinations of T1, T2*, TR, FA and θ. The proposed fitting method summarized in Figure 1 is composed of the following steps. In step 1, pseudo signal datasets were calculated by using function f with scan parameters (as shown in Table 1) and combinations of candidates for initial B1, T1 and T2* values (as shown in Table 2). In step 2, NCC (normalized cross-correlation) between signal datasets of images and pseudo signal datasets was calculated by following equation.
$$NC C=\frac{S_{m}\cdot S_{p}}{|S_{m}| |S_{p}|} (2),$$
where Sm is signal datasets of images, Sp is pseudo signal datasets. In step 3, the initial B1, T1 and T2* values were determined by extracting maximum NCC. In step 4, initial PD’ was calculated by following equation.
$$ PD'=\overline{\frac{S_{m}}{S_{p,i ni}}} (3),$$
where Sp,ini is pseudo signal datasets calculated by determined initial B1, T1, and T2* values. In step 5, T1, T2*, PD’ and B1 were estimated using Levenberg-Marquardt method (which is one of local optimization methods) with the predetermined initial values. In this process, spatial smoothing was executed to B1.
For evaluation, we compared the proposed method with conventional fitting method using simulated annealing method. A difference in MR parameter maps and computing time were evaluated. The difference in MR parameter maps was normalized by MR parameter maps obtained by the conventional method in region of white matter. Our computation platform was Windows 7 on Intel(R) Xeon(TM), 3.60 GHz.
Results
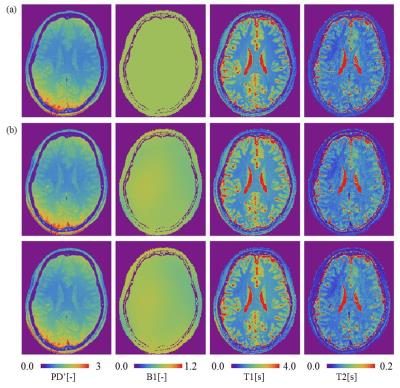
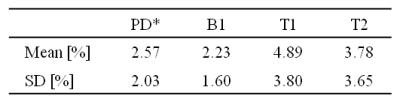
MR parameter maps of the predetermined initial values and MR parameter maps calculated by both proposed and conventional method are shown in Figure 2. The result shows that PD’, T1 and T2* maps of predetermined initial value were similar to these obtained by the proposed method. Furthermore, all of MR parameter maps obtained by the proposed method were quite similar to these obtained by conventional method. A difference of MR parameters between the proposed method and the conventional method are shown in Table 3. The difference was less than 5 %. On the other hand, a computing time of the proposed method was 8 min 32 s and it was approximately 15 times faster than the conventional method.Discussion
Generally, the local optimization method provides a faster fitting process than the global optimization method does, but tends to converge to a local solution. The proposed method avoids convergence on a local solution even though the local optimization method is used, because a neighborhood solution of a global optimal solution is extracted as the predetermined initial value. Thus, the proposed method can provide fast fitting process while maintaining calculation accuracy.Conclusion
We developed a fast fitting method for quantifying multiple MR parameters using local optimization method with predetermined initial values. The proposed method can calculate 3D multiple MR parameters 15 times faster than the conventional method.Acknowledgements
No acknowledgement found.References
1. European Society of Radiology (ESR), Magnetic Resonance Fingerprinting - a promising new approach to obtain standardized imaging biomarkers from MRIInsights Imaging. 2015; 6(2): 163–165.
2. Taniguchi Y, Yokosawa S, Bito Y. Simultaneous T1, T2, and B1 Mapping Using Partially RF-Spoiled Gradient Echo. In: Proceedings of the 19th Annual Meeting of the International Society for Magnetic Resonance Imaging. 2011;4560.
3. Taniguchi Y, Nakaya C, Bito Y, et al. A high-speed MRI simulator using the transition matrix method and periodicity of magnetization, Systems and Computers in Japan, 1995;26(2):54-62.
Figures