1432
Robust and fast phase unwrapping strategy to improve SWI quality1United Imaging of Healthcare America, Houston, TX, United States, 2Shanghai United Imaging of Healthcare, Shanghai, People's Republic of China
Synopsis
A robust and fast phase unwrapping strategy was developed for multi-echo SWI, to improve image quality where classic SWI fails, such as cavity vicinity regions, as well as to provide pristine field map for subsequent QSM applications. A smoothing and a seed prioritizing method were proposed, which was demonstrated to provide very robust unwrapping on phase difference map between neighboring echoes. And with a high quality unwrapped phase difference map, the phase of all echoes can be robustly unwrapped in seconds.
Purpose
Susceptibility weighted imaging (SWI) has been proven successful for imaging venography, microbleeds and iron/calcium deposition1. The prerequisite for creating high quality SWI is the proper preprocessing of phase images, which generally involves unwrapping phase aliasing and removing background field effects. The high-pass filter in classic SWI fails to remove rapidly changing background field effects (Fig. 2a). In principle, best-path region growing phase unwrapping methods2,3 can provide most accurate results when combined with proper background field removal methods such as SHARP4. However, the performance of best path unwrapping can be limited in low SNR regions due to the long TE, and the calculation time is long when multi-echo data are collected. Attempts have been made to achieve fast and robust phase unwrapping for multi-echo SWI, such as CAMPUS5 and UMPIRE6 , but these methods requir very short ΔTE between echoes to achieve virtually no phase aliasing in the phase difference map, thus limiting scanning parameters like resolution or readout bandwidth. Here we propose a practical strategy for fast and robust multi-echo phase unwrapping to improve multi-echo SWI quality.Methods
Assuming monopolar readout gradients was used, the first two echoes’ data were complex divided pixel-wisely, i.e. $$$\triangle\overrightarrow{S}=\overrightarrow{S}_{TE_{2}}/\overrightarrow{S}_{TE_{1}}$$$, which yielded an aliased phase difference map Δφ. Then $$$\triangle\overrightarrow{S}$$$ was smoothed to yield $$$\triangle\overrightarrow{S'}$$$ to yield a new phase difference map Δφ' with improved SNR. Here we found that the sphere mean value method7 with 6mm kernel provided a fast and satisfying result, but other smoothing methods may also work. Then a quality map of phase derivative variance was calculated on Δφ’, providing the best path guidance to unwrap Δφ’ 8. We improved the region growing strategy with seed prioritizing, such that during each iteration only the top 1% of current seed voxels with smallest phase derivative variance (or highest quality) will be used to unwrap their neighbors. With the smoothed, unwrapped Δφ'uw, the final unwrapped phase Δφuw can be obtained simply via $$$\triangle{φ}_{uw}=\triangle{φ}-[\frac{\triangle{φ}-\triangle{φ}_{uw}'}{2\pi}]\cdot{2\pi}$$$, where [] was a rounding operator. With Δφuw, the phase image of the nth echo can be unwrapped using $$${φ}_{uw}{(TE_{n})}={φ}{(TE_{n})}-[\frac{{φ}{(TE_{n})}-\triangle{φ}_{uw}'\cdot{TE_{n}}/(TE_{2}-TE_{1})}{2\pi}]\cdot{2\pi}$$$, with sub-second calculation speed.
If bipolar readout gradients were used, one can correct the eddy current terms between odd and even echoes5 first, then apply the above process similarly.
The multi-echo SWI scanning parameters in principle can be arbitrary. Data were collected on a 3T scanner (uMR 770, UIH, Shanghai, China) using a 24 channel head coil, and 6 echoes with TE from 4.5 to 26.8, ΔTE = 4.5ms, TR=32.2ms, FA = 15°, voxel size 1x1x2mm, matrix size 230x320x56, and monopolar readout gradients. All algorithms were implemented with Matlab on a 4-core 3.26GHz PC, and total computation time was ~80 seconds to yield unwrapped phase for all 6 echoes.
Results and Discussion
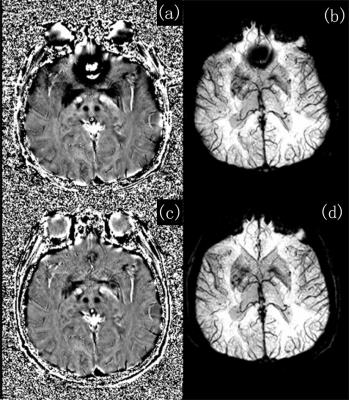
By integrating smoothing and seed prioritizing, we have significantly improved the robustness of the region growing phase unwrapping method, as demonstrated in Fig.1. And using the unwrapped phase difference map Δφuw, we obtained high quality phase maps for each echo (Fig.2c&2d) without any remnant phase artifacts seen in high-pass filtered phase and classic SWI images (Fig.2a&2b). The smoothing greatly reduced unwrapping errors by reducing noise, improving the phase continuity at low SNR regions such as scalps and cavity vicinity. Prioritizing the seed voxels, on the other hand, effectively prevents any remaining unwrapping errors from propagating, thus making the unwrapping process extremely robust. Previous region growing methods require skull stripping in order to remove low SNR regions such as non-tissue background and to provide well-defined edges for region growing stopping criteria. But non-tissue regions will not be an issue in our method. For example at air-tissue boundary, even voxels with partial tissue will have higher quality than air voxels, and the prioritizing makes sure that the tissue voxels be all processed way before proceeding onto air voxels, thus constraining the errors only among air voxels, as shown in the patching patterns in the air background in Fig.1d. By robustly unwrapping the phase difference map, a predicted phase at each TE can be estimated, and the original phase of each echo can be easily unwrapped by comparing with this predicted phase. Therefore regardless the number of echoes collected, the region growing unwrapping is only performed once on the phase difference map, significantly reducing the total computational time. Our new multi-echo phase unwrapping strategy is proven very robust and fast, it not only can be used for high quality SWI results, but can also benefit QSM by providing high quality and accurate field maps, which will be our future focus.Acknowledgements
No acknowledgement found.References
1. Haacke EM, Xu Y, Cheng YC, Reichenbach JR. Susceptibility weighted imaging (SWI). Magn Reson Med 2004;52(3):612-618.
2. Abdul-Rahman H, Arevalillo-Herraez M, Gdeisat M, Burton D, Lalor M, Lilley F, Moore C, Sheltraw D, Qudeisat M. Robust three-dimensional best-path phase-unwrapping algorithm that avoids singularity loops. Applied optics 2009;48(23):4582-4596.
3. Witoszynskyj S, Rauscher A, Reichenbach JR, Barth M. Phase unwrapping of MR images using Phi UN--a fast and robust region growing algorithm. Medical image analysis 2009;13(2):257-268.
4. Schweser F, Deistung A, Lehr BW, Reichenbach JR. Quantitative imaging of intrinsic magnetic tissue properties using MRI signal phase: an approach to in vivo brain iron metabolism? Neuroimage 2011;54(4):2789-2807.
5. Feng W, Neelavalli J, Haacke EM. Catalytic multiecho phase unwrapping scheme (CAMPUS) in multiecho gradient echo imaging: removing phase wraps on a voxel-by-voxel basis. Magn Reson Med 2013;70(1):117-126.
6. Robinson S, Schodl H, Trattnig S. A method for unwrapping highly wrapped multi-echo phase images at very high field: UMPIRE. Magn Reson Med 2014;72(1):80-92.
7. Li L, Leigh JS. High-precision mapping of the magnetic field utilizing the harmonic function mean value property. Journal of magnetic resonance 2001;148(2):442-448.
8. Abdul-Rahman HS, Gdeisat MA, Burton DR, Lalor MJ, Lilley F, Moore CJ. Fast and robust three-dimensional best path phase unwrapping algorithm. Applied optics 2007;46(26):6623-6635.
Figures