1423
Multi-contrast image guided graph representation and its application in compressed sensing MRI reconstruction1Dept. of Communication Engineering, Fujian Provincial Key Laboratory of Plasma and Magnetic Resonance, Xiamen University, Xiamen 361005, China, xiamen, People's Republic of China, 2Dept. of Electronic Science, Fujian Provincial Key Laboratory of Plasma and Magnetic Resonance, Xiamen University, Xiamen 361005, China, People's Republic of China, 3Dept. of Computer Science, Xiamen University of Technology, Xiamen 361024, China, People's Republic of China
Synopsis
Under-sampling the k-space data and reconstructing images with sparsity constraint is one efficient way to accelerate magnetic resonance imaging However, achieving high acceleration factor is challenging since image structures may be lost or blurred when the sampled information is not sufficient. In this work, we propose a new approach to reconstruct magnetic resonance images by learning the prior knowledge from multi-contrast images with graph-based sparsifying transform. To incorporate extra information from multi-contrast image, registration is included in a bi-level optimization frame as well as the sparse reconstruction. Experiment results demonstrate that the proposed method outperforms the state-of-art with high accelerating factor.
Purpose
Accelerating the imaging speed without sacrificing image structures plays an important role in magnetic resonance imaging. Under-sampling the k-space data and reconstructing the image with sparsity constraint is one of efficient ways to reduce the data acquisition time 1,2. However, achieving high acceleration factor is challenging since image structures may be lost or blurred when the sampled information is not sufficient. Therefore, incorporating extra knowledge to improve image reconstruction is expected for highly accelerated imaging. Fortunately, multi-contrast images in the same region of interest are usually acquired in magnetic resonance imaging protocols 3. In this work, we propose a new approach to reconstruct magnetic resonance images by learning the prior knowledge from these multi-contrast images with graph-based representations. We further formulate the reconstruction as a bi-level optimization problem to allow misalignment between these images.Methods
The under-sampling of k-space data in MR imaging can be expressed as: $$${\bf{y}} = {\bf{UFx}} + {\bf{\varepsilon }}$$$, where $$${\bf{y}}$$$ denote the under-sampled k-space data, $$${\bf{U}}$$$ and $$${\bf{F}}$$$ denote the under-sampling and Fourier transform respectively, denote the target image to be recovered and $$${\bf{x}}$$$ denote the noise vector. To incorporate the prior information from multi-contrast image, registration between different contrast image is needed. The registration 4 can be achieved by maximizing the mutual information(MI) between the reference image $$${{\bf{x}}_{ref}}$$$ and the target image $$${\bf{x}}$$$. Then, the registration and sparse reconstruction can be formulated as a bi-level optimization problem: $$\eqalign{ & {\rm{P}}1:\mathop {\max }\limits_{{{\bf{x}}_{ref}}} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathop{\rm MI}\nolimits} ({{\bf{x}}_{ref}}{\bf{,x}}) \cr & {\rm{P}}2:\mathop {\min }\limits_{\bf{x}} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\left\| {{{\bf{\Psi }}_{{\rm{MG\_R}}}}{\bf{x}}} \right\|_1}\matrix{ {} & {s.t.} \cr } \left\| {{\bf{y}} - {\bf{UFx}}} \right\|_2^2 \le {\sigma ^2} \cr} $$
where the P1 problem maximize mutual information to obtain the registered multi-contrast image. The sparsifying transform $$${{\bf{\Psi }}_{{\rm{MG\_R}}}}$$$ is trained from the registered multi-contrast image adaptively.
The P2 problem is to solve the constrained convex optimization with a nonlinear algorithm. The flow chart is shown in Fig. 1. Projected fast iterative soft-thresholding algorithm ( pFISTA) is chosen to solve P2 problem for its advantage of efficient computing, fast convergence and nearly free of parameter tuning 5.
Results
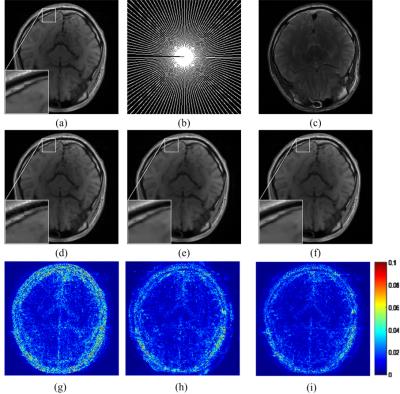
The MRI images acquired from SIMENS MAGNETOM Trio Tim are used to evaluate the performance of the proposed method. The proposed method is compared with two state-of-the-art CS-MRI reconstruction methods that also use multi-contrast images as reference: Compressed sensing MRI using patch-based nonlocal operator (PANO) 6 with multi-contrast image and Bayesian compressed sensing (BCS) with prior estimate 7,8 . The relative l2-norm error (RLNE) defined as: $$$e(\mathbf{\hat{x}})\mathbf{=}{{{{{\left\| \mathbf{\hat{x}-\tilde{x}} \right\|}_{\mathbf{2}}}}/{\left\| {\mathbf{\tilde{x}}} \right\|}\;}_{\mathbf{2}}}$$$ denotes the fully sampled image, is estimated as a measure of the difference between the reconstructed image and the fully sampled image.
The reconstructed images in Fig. 2 demonstrate that the proposed method outperforms the other two methods in detail preservation Reconstructed details using BCS are mottled and the PANO reconstruction seems over-smoothed. The magnitude errors indicate that the proposed method leads reconstructed image with higher consistency to the ground truth.
Conclusion
A MRI image reconstruction method by incorporating prior information from multi-contrast reference images is proposed in this work. The prior information is embedded into the graph wavelet-based image sparse representation learnt from the reference image and this information updated with better accuracy by iteratively registering the reference image to the target one. Results on realistic MRI images implies that incorporating multi-contrast images can significantly improve the reconstruction and the iteration between registration and reconstruction is necessary when the acquired is very limited. The proposed approach would be meaningful for highly accelerated MRI imaging.Acknowledgements
This work was supported by National Natural Science Foundation of China (61571380, 11375147 and 61302174), Natural Science Foundation of Fujian Province of China (2015J01346, 2016J05205), Fundamental Research Funds for the Central Universities (20720150109), Important Joint Research Project on Major Diseases of Xiamen City (3502Z20149032).
The correspondence should be sent to Dr. Xiaobo Qu (Email: quxiaobo@xmu.edu.cn)
References
1. M. Lustig, D. Donoho, and J. M. Pauly, "Sparse MRI: The application of compressed sensing for rapid MR imaging," Magnetic Resonance in Medicine, 58, 1182-95, 2007.
2. M. Lustig, D. L. Donoho, J. M.Santos, and J. M. Pauly, "Compressed sensing MRI," IEEE Signal Processing Magazine, 72, 72-82, 2008.
3. J. Huang, C. Chen, and L. Axel, "Fast multi-contrast MRI reconstruction," Magnetic Resonance Imaging, 32, 1344-1352, 2014.
4. J. P. W. Pluim, J. B. A. Maintz, and M. A. Viergever, "Mutual-information-based registration of medical images: A survey," IEEE Transactions on Medical Imaging, 22, 986-1004, 2003.
5. Y. Liu, Z. Zhan, J.-F. Cai, D. Guo, Z. Chen, and X. Qu, " Projected iterative soft-thresholding algorithm for tight frames in compressed sensing magnetic resonance imaging," IEEE Transactions on Medical Imaging, 35, 2130-2140, 2016.
6. X. Qu, Y. Hou, F. Lam, D. Guo, J. Zhong, and Z. Chen, "Magnetic resonance image reconstruction from undersampled measurements using a patch-based nonlocal operator," Medical Image Analysis, 18, 843-856, 2014.
7. B. Bilgic and E. Adalsteinsson, "Joint bayesian compressed sensing with prior estimate," ISMRM 2012.
8. B. Bilgic, V. K. Goyal, and E. Adalsteinsson, "Multi-contrast reconstruction with Bayesian compressed sensing," Magnetic Resonance in Medicine, 66, 1601-15, 2011.
Figures