Synopsis

Non-uniformly sampling is an effective way to accelerate high-dimensional magnetic resonance spectroscopy (MRS). The spectrum is usually reconstructed with proper prior knowledge. In this work, we exploit the intrinsic N-D exponential signals of multi-dimensional MRS to reconstruct the spectrum. A low rank tensor representation of multi-dimensional MRS and the exponential structure of the associated factors are simultaneously explored. Results on 3-D MRS data shows that the proposed method can faithfully reconstruct the spectrum from a small amount of measurements, allowing a significant reduction of acquiring time in real applications.

Purpose

The sampling time of multi-dimensional MRS increases exponentially lasting from hours to days. The non-uniform sampling technique is an effective way to accelerate the MRS sampling process, and the missing data is reconstructed with proper signal priors. Qu et al exploited the exponential characteristic of time domain signals in MRS and proposed the low rank Hankel matrix completion (LRHMC) ¹, which has been shown that LRHMC has the advantage in recovering broad peaks compared with compressed sensing ¹. However LRHMC is limited to recovery 2-D MRS. This work extends LRHMC to recover multi-dimensional (>=3D) MRS by simultaneously exploring the low rank tensor structure and exponential structure in time domain MRS.

Method

We first model the time domain signal of MRS $$${{\cal Y}}$$$ as a CP tensor ² and each factor is an exponential function ^1,3,

$${ {{\cal Y}}= {\sum\limits_{r = 1}^{ R} {{\bf{u}}_r^{\left( 1 \right)} \circ {\bf{u}}_r^{\left( 2 \right)} \circ \ldots \circ {\bf{u}}_r^{\left( N \right)}} }}$$

where $$${\bf{u}}_{r}^{( n )}$$$ is the factor from CP tensor which has the exponential structure and $$$ \circ $$$ denotes the outer product of some vectors. To promote the exponential structure of the factors, we adopt the fact that the Hankel matrices induced by the factors $$${\bf{u}}_{{r}}^{( {{n}} )}$$$ of tensor $$${{\cal Y}}$$$ are of rank 1. To be more precise, define a linear operator $$${{\cal R} }{\rm{: }}{\mathbb{C}^{{I_n}}} \to {\mathbb{C}^{S_1^{ {\kern 2pt}( n )} {\kern 2pt} \times S_2^{ {\kern 2pt}( n )}}}$$$, for some integers $$$S_1^{( n )}$$$ and $$$S_2^{( n )}$$$ satisfying $$$S_1^{( n )} + S_2^{( n )} = {I_n} + 1$$$ , as follows

$${\left[ {{{\cal R}}{\bf{u}}_r^{\left( n \right)}} \right]_{k,l}} = {\left[ {{\bf{u}}_r^{\left( n \right)}} \right]_{k + l - 1}}{\rm{, }}\forall {\rm{ }}1 \le k \le S_1^{\left( n \right)}{\rm{,}}1 \le k \le S_2^{\left( n \right)}.$$

Then, the rank of $$${{\cal R}}{\bf{u}}_r^{( n)}$$$ is 1 for any $$$r = 1,...,R$$$ and $$$n = 1,...,N$$$ because of exponential structure. Therefore, we add the low-rank constraints on the Hankel matrices formed by the factors into the least squares low rank tensor completion to get

$$\mathop {{\rm{min}}}\limits_{\scriptstyle{\bf{u}}_r^{\left( n \right)} \atop { r = 1,...,\hat R \atop \rm{n = 1,}...{\rm{,}}N}} {\rm{ }}{\sum\limits_{r = 1}^{\hat R} {\sum\limits_{n=1}^N {\left\| {{{\cal R}}{\bf{u}}_r^{\left( n \right)}} \right\|_*} } } + \frac{\lambda }{2}\left\| {{{{\cal P}}_\Omega }\left( {\sum\limits_{r = 1}^{\hat R} {{\bf{u}}_r^{\left( 1 \right)} \circ {\bf{u}}_r^{\left( 2 \right)} \circ \ldots \circ {\bf{u}}_r^{\left( N \right)}} } \right) - {{{\cal P}}_\Omega }{{\cal Y}}} \right\|_F^2,$$

where $$$\hat R$$$ denotes an estimation of $$$R$$$ which is the number of exponentials, $$${\bf{u}}_r^{\left( n \right)}$$$ is the factors of tensor, $$${{{\cal P}}_\Omega }$$$ denotes performing under sampling on tensor $$${{\cal Y}}$$$, $$${\left\| \cdot \right\|_*}$$$ denotes the nuclear norm, and $$$\lambda $$$ is the regularization parameter that trades off the nuclear norm against the data consistency. We refer to the proposed model as Hankel Matrix nuclear norm Regularized low rank Tensor Completion (HMRTC).

Result

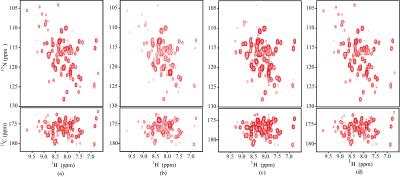
Here we apply the proposed HMRTC to recover a three dimensional (3D) spectrum with the size of $$$64 \times 128 \times 512$$$ from a 3D Poisson gap non-uniformly sampled time-domain data.The experiment was carried out on a Bruker AVANCE III 600 MHz spectrometer equipped with a cryogenic probe at 293K. Spectra are processed in NMRPipe using a routine processing manner. The skyline projection spectra, plotted by summing all the frequency points along the rest dimensions, is used here to simplify the description of spectra. Figure 1 shows the ¹H-¹⁵N and ¹H-¹³C skyline projection spectra of HNCO spectrum for the U-[¹⁵N, ¹³C] RNA recognition motifs domain of protein RNA binding motif protein 5, which is a component of the spliceosome A-complex. Obviously, the HMRTC produces the most faithful recovery (Fig. 1(d)) of the ground truth (Fig. 1(a)) than ADM-TR ⁴ (Fig. 1(b)) and WCP ⁵ (Fig. 1(c)). Moreover, Fig. 1(d) indicates that HMRTC can achieve high quality of reconstruction even with the 10% sample ratio and hence allow a significant reduction in measurement time. All together, the proposed HMRTC algorithm may serve as a versatility method for studying biological or chemical molecules using N-D NMR spectroscopy.

Conclusion

Acknowledgements

This work was supported by National Natural Science Foundation of China (61571380, 11375147 and 61302174), Natural Science Foundation of Fujian Province of China (2015J01346, 2016J05205), Fundamental Research Funds for the Central Universities (20720150109), Important Joint Research Project on Major Diseases of Xiamen City (3502Z20149032).

The correspondence should be sent to Dr. Xiaobo Qu (Email: quxiaobo@xmu.edu.cn)

References

1. X. Qu, M. Mayzel, J.-F. Cai, Z. Chen, and V. Orekhov, Accelerated NMR spectroscopy with low-rank reconstruction, Angewandte Chemie International Edition, 54:852-854, 2015.

2. V. Orekhov and V. A. Jaravine, Analysis of non-uniformly sampled spectra with multi-dimensional decomposition, Prog. Nucl. Magn. Reson. Spectrosc., 59:271-292, 2011.

3. H. M. Nguyen, X. Peng, M. N. Do, Z.-P. Liang, Denoising MR spectroscopic imaging data with low-rank approximations, IEEE Transactions on Biomedical Engineering, 60:78-89, 2013.

4. S. Gandy, B. Recht, and I. Yamada, Tensor completion and low-n-rank tensor recovery via convex optimization, Inverse Probl., 27:25010-25028, 2011.

5. E. Acar, D. M. Dunlavy, T. G. Kolda, and M. Mørup, Scalable tensor factorizations for incomplete data, Chemometrics and Intelligent Laboratory Systems, 106: 41-56, 2011.