1418
A low rank Hankel matrix reconstruction approach to recover hybrid time and frequency data in non-uniformly sampled magnetic resonance spectroscopy1Department of Electronic Science, Xiamen University, Xiamen, People's Republic of China, 2School of Computer and Information Engineering, Xiamen University of Technology, Xiamen, People's Republic of China
Synopsis
Magnetic resonance spectroscopy has many important applications in bio-engineering while the acquisition of high dimensional spectroscopy is usually time consuming. Non-uniformly sampling can speed up the data acquisition but the missing data points have to be restored with proper signal models. In this work, a specific two dimensional magnetic resonance signal, of which the first dimension lies in time domain while the second dimension lies in frequency domain, is reconstructed with a proposed low rank enhanced Hankel matrix method. Results on realistic magnetic resonance spectroscopy shows that proposed method outperform the state-of-art compressed sensing method on recovering low intensities spectral peaks.
Purpose
High resolution and multi-dimensional magnetic resonance spectroscopy (MRS) suffers from long acquisition time. The spatio-temporally encoded ultrafast (STEU) strategy decreases the acquisition time significantly, but it demands strong acquisition gradient which may do harm to the spectrometer 3. Non-uniform sampling has been applied to alleviate the demand of strong acquisition gradient, however, signal may be lost in hybrid time and frequency (HTF) plane and shrinkage of peaks could be observed in reconstructed spectrum by CS 1-5. Therefore, we proposed a new hybrid time and frequency signal recovery model which produces faithful reproduction of weak intensity peaks for fast MRS. In addition, the proposed method is applicable to recover any signal of which can be modeled as a sum of exponential functions in bio-engineering applications, e.g. signal enhancement, feature extraction and fast sampling.Method
The rank of an enhanced matrix constructed from a sum of two dimensional (2D) exponential functions equals the number of exponential functions, i.e., the number of spectral peaks, of a 2D spectrum 6. The number of peaks has been observed to be much smaller than its ambient dimension, implying that the rank of the enhanced matrix is low 7,8 . The low rank Hankel matrix properties have been applied in MRSI denoising 7 and fast sampling 8 of MRS. In this work, we attempt to explore those nice properties 6,7 and propose the following low rank Hankel reconstruction model to restore HTF signals
$$\mathop {{\rm{min}}}\limits_{\bf{G}} {\rm{ }}{\left\| {{\bf{BF}}_{freq}^{ - 1}{\bf{G}}} \right\|_ * } + \frac{\lambda }{2}\left\| {{\bf{Y}} - {{\bf{P}}_\Omega }{\bf{G}}} \right\|_F^2,$$
where $$$\bf{G}$$$ denotes a 2D acquired hybrid time and frequency signal in STEU MRS; $$${\bf{F}}_{freq}^{ - 1}$$$ denotes the 1D inverse Fourier transform along the frequency dimension; $$$\bf{B}$$$ is the operator that constructs an block Hankel matrix; $$$\bf{Y}$$$ the acquired HTF signal; $$${{\bf{P}}_\Omega }$$$ the operator that undersamples 2D signal; $$${\left\| \cdot \right\|_ * }$$$ denotes the nuclear norm (sum of singular values) of a matrix; $$${\left\| \cdot \right\|_F}$$$ denotes the Frobenius norm; and the parameter $$$\lambda$$$ tradeoffs between the nuclear norm and data consistency.
Result
We utilized a 2D liver oil spectrum adopting STEU technology to validate the proposed method, and the method is compared with the state-of-art CS method 3. The experiments are carried out on a Varian 500 MHz NMR System (Agilent Technologies,Santa Clara, CA, USA) equipped with a 5-mm indirect detection probe. Acquisition parameters for the experiment included:encoding gradients = 3.91 G/cm, decoding gradients = 48.8 G/m, compensative gradient = -7.81 G/cm, duration of eachdecoding gradient lobe (TD) = 220 us, duration of the chirp pulse (t1mix) = 12ms, duration of compensative gradient =0.5 ms, and number of alternating gradient pairs (ND) = 150. The WURST profile with the sweep frequency range of 30kHz in 6ms.
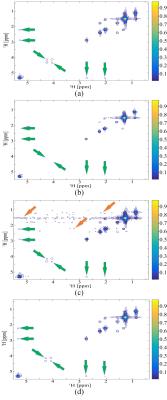
The fully measured 2D STEU MRS signal is of size $$$200 \times 100$$$, where the first dimension is the frequency dimension while the other is the time dimension. The fully sampled 2D spectrum is shown in Figure 1 (a). The hybrid time and frequency signal is subsampled with a Poisson Gap mask 8 with 20% data points measured.
Figure 1 shows the reconstructed spectrum. Eight low intensity peaks are weaken or missed in CS reconstruction (green arrows in Figure 1 (b)). To observe these weaken signals, one may increase the contour levels, but pseudo peaks also comes up (yellow arrows in Figure (c)). In contrast, these low intensity peaks are reconstructed much better using the proposed method. Experiment on STEU COSY implies that the proposed method outperforms CS in term of reproduction of low intensities peaks.
Conclusion
We proposed a low rank Hankel matrix reconstruction method for hybrid time and frequency data recovery. To exploite the low rank property of 2D signal, we construct a block Hankel matrix by using time domain exponential signals converted from hybrid time frequency signal and a low rank assumption is made on block Hankel matrix to recover hybrid time and frequency signals. Experimental results show that the proposed approach can provide faithful reconstruction and outperform the state-of-art compressed sensing approach in terms of weak intensity peaks.Acknowledgements
This work was supported by the National Natural Science Foundation of China (61571380, 61302174 and 11375147),Natural Science Foundation of Fujian Province of China (2015J01346 and 2016J05205), Important Joint Research Project on Major Diseases of Xiamen City (3502Z20149032), Fundamental Research Funds for the Central Universities (20720150109).
The correspondence should be sent to Dr. Xiaobo Qu (Email: quxiaobo@xmu.edu.cn)
References
1. X. Qu, et al., Compressed sensing for sparse magnetic resonance spectroscopy, ISMRM 2010, 3371.
2. X. Qu, et al., Reconstruction of self-sparse 2D NMR spectra from undersampled data in indirect dimension, Sensors, 2011, 11, 8888-8909.
3. Y. Shrot and L. Frydman, Compressed sensing and the reconstruction of ultrafast 2D NMR data: Principles and biomolecular applications, Journal of Magnetic Resonance, 2011; 209(2):352-358.
4. D.J. Holland, et al., Fast multidimensional NMR spectroscopy using compressed sensing. Angewandte Chemie International Edition, 2011, 50, 6548-6551.
5. K. Kazimierczuk, et al., Accelerated NMR spectroscopy by using compressed sensing. Angewandte Chemie International Edition,2011, 50, 5556-5559.
6. Y. Hua, Estimating two-dimensional frequencies by matrix enhancement and matrix pencil, IEEE Transactions on Signal Processing, 1992; 40, 2267-2280.
7. H. M. Nguyen, et al., Denoising MR spectroscopic imaging data with low-rank approximations, IEEE Transactions on Biomedical Engineering, 2013, 60, 78-89.
8. X. Qu, et al., Accelerated NMR spectroscopy with low-rank reconstruction, Angewandte Chemie International Edition, 2015, 54, 852-854.
9. S. G. Hyberts, et al., Application of iterative soft thresholding for fast reconstruction of NMR data non-uniformly sampled with multidimensional Poisson Gap scheduling, Journal of Biomolecular NMR, 2012, 52, 315-327.
Figures