1415

Accelerated MR Diffusion Tensor Imaging Using Partial Fourier Compressed Sensing

Chia-Chu Chou¹, Frank Q Ye², Cecil Chern-Chyi Yen³, Behtash Babadi¹, Rao P Gullapalli⁴, David A Leopold², and JiaChen Zhuo⁴

¹ECE, University of Maryland College Park, College Park, MD, United States, ²Neurophysiology Imaging Facility, National Institute of Mental Health, National Institute of Neurological Disorders and Stroke, and National Eye Institute, National Institutes of Health, Bethesda, MD, United States, ³NINDS/LFMI/CMS, National Institutes of Health, Bethesda, MD, United States, ⁴Diagnostic Radiology and Nuclear Medicine, UM School of Medicine, Baltimore, MD, United States

Synopsis

3D-DTI are often used in ex vivo imaging to achieve superior spatial resolution and to map fine white matter structure. However, image acquisition time is long especially when many diffusion directions are used to better define orientation profiles and resolve crossing fibers. In this study we apply a new imaging acceleration technique – Partial Fourier Compressed Sensing (PFCS) on DTI acceleration. We demonstrated PFCS provide satisfactory reconstruction with only half of the raw data while retaining fine anatomical details on DTI parameter maps.

Introduction

Diffusion MRI (dMRI) is a powerful technique for imaging brain white matter fiber orientation and connection ¹. When used on ex vivo brain samples, dMRI can achieve high spatial resolution with 3D acquisition sequence and reveal very fine anatomical details ^2-4. The drawback of a 3D sequence is its long acquisition time. While six images of different diffusion direction are sufficient to define a diffusion tensor, tens or even hundreds diffusion directions are needed to better define the diffusion orientation profiles and to resolve crossing fibers. When combined with 3D acquisition, the total dMRI acquisition time in an ex vivo brain study can be up to a few days. We previously proposed an image acceleration method – Partial Fourier Compressed Sensing (PFCS) in the context of Electron Paramagnetic Resonance Imaging (EPRI) acceleration ⁵. In this study we explore the extension of this method to accelerate 3D DTI acquisition.

Experiments

To test the algorithm we used existing data from a fixed monkey brain sample. The procedure followed a standard protocol ⁴ in a 7-Tesla Bruker scanner. The diffusion data acquisition used a 3D spin-echo diffusion weighted echo planar imaging (EpiDti) sequence available in Bruker Paravision software. Twenty six diffusion directions were acquired at b = 4800 s/mm² and three volumes at b=0. The 3D image had an isotropic spatial resolution of 0.25mm (320 × 278 × 256). The data set was obtained with 60% of the views in phase encoding direction in order to keep echo time short (31.5 msec), while the read and slice direction were fully acquired. Partial Fourier reconstruction was employed for image reconstruction. These images served as the ground truth when comparing with the PFCS technique.

Methods

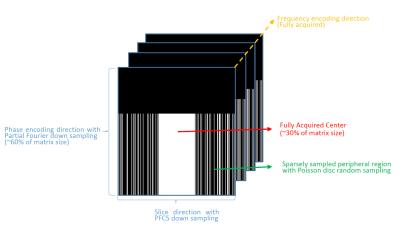
PFCS is an image acceleration technique which apply conjugate symmetry property of k-space with compressed sensing reconstruction ⁵. To test the efficacy of the PFCS reconstruction on 3D-DTI dataset, we further under-sampled the k-space in the slice direction. We divided the data into two partitions: a large fully-sampled area in the center (30% of matrix size) with the rest sparsely sampled with Poisson disc random sampling in a manner that resulted in 50% under sampling (see Fig 1). Furthermore, to eliminate erroneous phase map estimation for each DWI, we use POCS ^5,6 (Projection Onto Convex Sets) method to estimate the phase map from the data after down sampling on slice dimension. Performance of PFCS reconstruction and compressed sensing (CS) reconstruction were compared with the original partial Fourier reconstructed images (Ground Truth) and comparisons were made regarding image quality and normalized mean square error (nMSE), which is defined by $$$\sqrt{\frac{||ReconstructedImage - Ground Truth||^2}{||Ground Truth||^2}}$$$.We also compared parameter maps from fitting data to the diffusion tensor mode.

Results

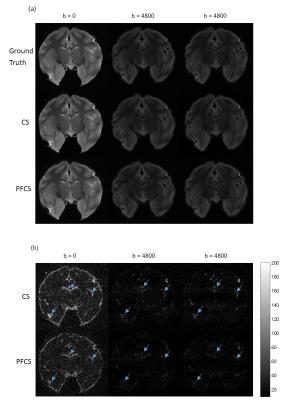
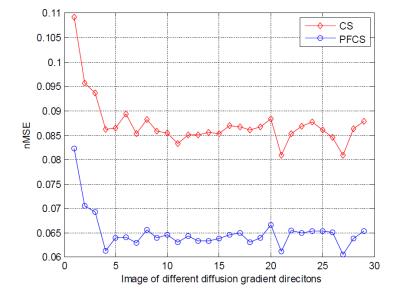
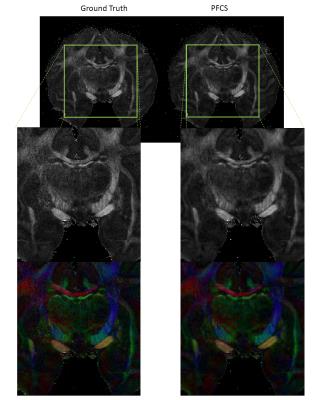
Fig. 2 shows the comparison of conventional CS and PFCS on DWIs. Fig. 2(a) shows the Ground Truth, CS, and PFCS reconstructed DWIs on several different diffusion gradient directions. The difference maps of CS vs. Ground Truth and PFCS vs. Ground Truth are displayed in Fig. 2(b). From the figure we can clearly see the improvement of PFCS reconstructed image compared to CS, especially in some boundary areas (blue arrow). Fig. 3 shows the nMSE of all DWIs. PFCS outperforms CS in all the diffusion gradient directions. Fig. 4 presents the FA and color-coded principal diffusion direction maps generated from Ground Truth and PFCS reconstructed DWIs respectively. Some smoothness was introduced due to the PFCS reconstruction, which leads to a more smoothed FA map. However PFCS preserved almost all the details of the raw FA map, as well as accurately captured the principle diffusion direction.

Discussion

We demonstrated that PFCS can double the acceleration rate in 3D DTI scans by acquiring only 50% of data on the slice dimension. The missing data are well compensated in PFCS by deriving them from the conjugate symmetry of the k-space. PFCS reconstructed FA maps is less noisy than Ground Truth because of the natural smoothing property of compressed sensing reconstruction. Although denoising usually accompanies with loss of resolution, this is shown to be tolerable in FA and principle direction map estimation where fine structure details are well kept. Future work will continue to optimize this technique to obtain better spatial resolution and acceleration rate.

Acknowledgements

No acknowledgement found.

References

1. W.V. Hecke, L Emsell, S. Sunaert, Diffustion Tensor Imaging, New York: Springer Scientice Business Media, 2016.

2. D’Arceuil HE, Westmoreland S, de Crespigny AJ, "An approach to high resolution diffusion tensor imaging in fixed primate brain," Neuroimage, vol. 35, no. 2, pp. 553-565, 2007.

3. Wedeen VJ, et al., "Diffusion spectrum magnetic resonance imaging (DSI) tractography of crossing fibers," Neuroimage, vol. 41, no. 4, pp. 1267-1277, 2008.

4. Reveley C et al., "Superficial white matter fiber systems impede detection of longrange cortical connections in diffusion MR tractography," PNAS, vol. 112, no. 21, pp. 2820-2828.

5. C.C Chou, C. Cadisetti, T. Shin, N. Devasahayam, A. McMillan, B. Babadi, R. Gullapalli, M. Cherukuri, J. Zhuo, "Accelerated electron paramagnetic resonance imaging using partial Fourier compressed sensing reconstruction," Magnetic Resonance Imaging (In Press), 2016.

6. J. Pauly, "Partial K-space reconstruction".Stanford University.

Figures

Figure 1: The sampling mask specified for DTI. For the frequency encoding direction (shown in orange dash arrow), the data are fully acquired. For the phase encoding dimension, raw data have included Partial Fourier down sampling (~60% of matrix size). For the slice dimension, the data points are divided into fully acquired center and Poisson disc sparsely sampling peripheral. In total only 30% of k-space points are used in PFCS reconstruction. (60% on phase encoding dimension, and 50% on slice dimension)

Figure 2: The comparison of conventional CS and PFCS on DWIs. The image magnitude of several DWIs is displayed in (a). The PFCS images are less blurring and able to preserve more details than CS. The difference maps are given in (b). From (b) we can easily observe the improvement of PFCS reconstructed images, especially in some boundary areas (blue arrow).

Figure 3: The nMSE of DWIs of all the 26 diffusion gradient directions as well as 3 b0 images (The first three points). Obviously, PFCS outperforms CS in every DWIs.

Figure 4: The FA and the Principal Diffusion Direction Map from Ground Truth and PFCS-DWIs. It is clear that PFCS preserved almost all the details of the Ground Truth FA map, including tiny fibers. Meanwhile, it accurately captured the principle diffusion direction. However, PFCS FA map is smoother due to the natural smoothing property of reconstruction.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)

1415