1414
Accelerated 3D Arterial Spin Labeling using Cartesian Acquisition with Spiral Reordering and Compressed Sensing1Radiology, UT Southwestern Medical Center, Dallas, TX, United States, 2Bioengineering, UT Dallas, Dallas, TX, United States, 3Advanced Imaging Research Center, UT Southwestern Medical Center, Dallas, TX, United States
Synopsis
Arterial spin labeling (ASL) is a non-contrast perfusion imaging method for MRI. However, 2D ASL suffers from low signal to noise ratio. 3D ASL is favorable to overcome the limitation of 2D ASL, but 3D acquisition is time-consuming, so acceleration of 3D ASL is highly desired. The new compressed sensing (CS) theory allows perfect reconstruction far below Nyquist rate. We implemented a novel 3D TSE acquisition using Cartesian Acquisition with SPiral Reordering (CASPR), which can be undersampled and combined with CS. Preliminary results show improved image quality using 3D Sparse-BLIP reconstruction that is comparable to fully sampled acquisition.
INTRODUCTION
Arterial spin labeling (ASL) is a quantitative non-contrast perfusion imaging method that can be performed on standard MRI equipment [1]. However, 2D ASL suffers from low signal to noise ratio (SNR) and requires multiple signal averages. The higher SNR and increased volume coverage afforded by 3D acquisitions can overcome certain limitations of 2D acquisitions. Hence, the consensus paper on brain perfusion suggested using TSE/GraSE acquisition with 3D spiral trajectories. However, these acquisitions are still long (e.g. 5~7 minutes) for whole brain coverage and can benefit from shortened acquisitions. The sparse signal of the ASL images renders it to be readily applicable with emerging compressed sensing (CS) theory [2-5]. However, the extension of CS algorithms to non-Cartesian acquisitions is non-trivial [6]. In this work, we implemented a novel 3D TSE acquisition using Cartesian Acquisition with SPiral Reordering (CASPR), which can be readily undersampled and combined with CS reconstruction.METHODS
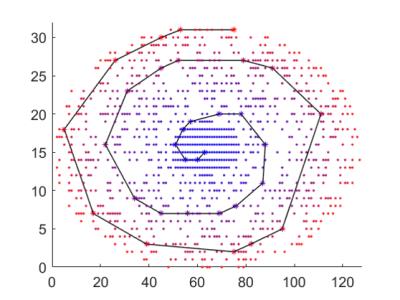
Acquisition: The 3D CASPR view ordering that can be performed with a pseudo-random undersampling was implemented on a 3T Philips Ingenia scanner. Each shot of the 3D TSE echo train begins from the center of the k-space and traverses spirally outwards, yet sampling on the Cartesian ky-kz grid. The k-space was downsampled with a pseudo random undersampling and segmented into multiple spiral interleaves in ky-kz plane (Fig. 1). By sampling the center of k-space at the beginning of each echo train, this approach increases the efficiency of capturing the ASL prepared signal. The fully sampled central part of the k-space can be used for sensitivity estimation. Due to the sampling on the Cartesian grid, this sampling approach can be readily reconstructed using fast Fourier transformations and combined with CS. CS reconstruction was first evaluated on a brain proton density weighted image acquired using the fully sampled k-space with CASPR trajectory. Subsequently, ASL images were acquired using pseudo-continuous labeling and acquired with a fully sampled CASPR trajectory. In both cases, CS reconstruction was evaluated by retrospectively undersampling the k-pace. Finally, 3D pCASL images of the brain were acquired using an undersampled CASPR trajectory with a reduction factor R=3, as shown in Fig. 1. Imaging parameters were: TR/TE=6000/12ms, FOV=200x200x160 mm3, matrix=80x80 with 52 slices of 6 mm slices, reconstructed to 3mm slices. Total acquisition time was 6 minutes for fully sampled acquisition and 2 minutes for R=3 undersampled acquisition.
Reconstruction: Sparse-BLIP [7] provides a framework for image reconstruction without knowledge of coil sensitivities. We extended the original 2D Sparse-BLIP method to 3D, where 3D sparsity was considered and sparse constraint was calculated in the x-y-z domain. The objective equation was defined as: $$$\min_{S_l,f}\sum_l\parallel F(S_lf)-d_l\parallel_2^2+\alpha \parallel \Psi(f)\parallel_1+\beta \sum_l \parallel S_l \parallel_2^2$$$, where $$$f$$$ is the desired 3D images and $$$S_l$$$is coil sensitivity map from the l-th coil, $$$ F $$$ is the undersampling Fourier operator, $$$d_l$$$ is the undersampled 3D k-space data from the l-th coil, $$$\Psi(\cdot)$$$ is the 3D sparse transform operator, such as the 3D total variation (TV) operator or 3D wavelet operator, and we chose 3D TV considering the running efficiency, $$$\parallel \cdot \parallel _1$$$ is the L1-norm to constraint on the sparsity of images, $$$\parallel \cdot \parallel _2^2$$$ is the L2-norm to constraint on the smooth property of the sensitivity, $$$\alpha$$$ and $$$\beta$$$ are regularization parameters.
Results and Discussion
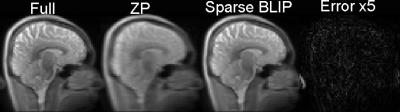
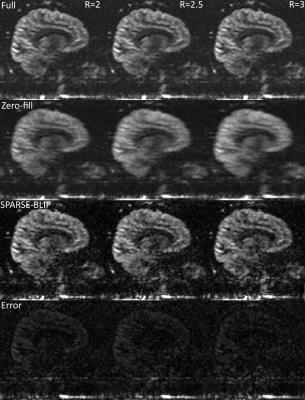
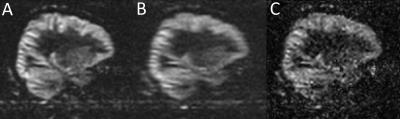
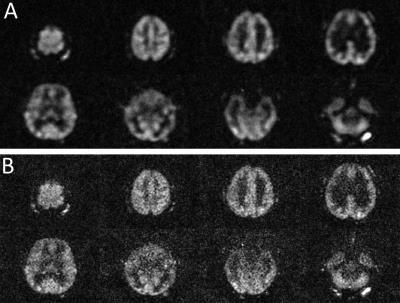
Fig. 2 shows the feasibility of 3D Sparse-BLIP reconstruction as applied to a fully sampled proton density weighted brain image, which was retrospectively undersampled by a factor of 3. Fig. 3 shows the 3D pCASL images acquired with a fully sampled CASPR trajectory that was undersampled retrospectively with factors of 2, 2.5 and 3. The zero-filled images show more blurring, which were successfully reconstructed using 3D Sparse-BLIP to increase spatial resolution. Compared to fully sampled images, there was minimal error with some loss of details. Fig. 4 compares a fully sampled image (6 min acquisition) with an undersampled image using a factor of 3 (2 min acquisition) using zero-filled reconstruction and using 3D Sparse-BLIP reconstruction. Fig. 5 shows multiple slices of the axial reformats from the undersampled ASL image using zero-filling (Fig. 5A) and 3D Sparse-BLIP reconstruction (Fig. 5B), which was acquired in 2 minutes.Conclusion
We implemented an efficient 3D Cartesian Acquisition using SPiral Reordering (CASPR) method for ASL perfusion that can be readily undersampled and combined with CS. Preliminary results show improved image quality using 3D Sparse-BLIP based CS reconstruction that is comparable to fully sampled acquisition. Future optimization will include different undersampling patterns, such as Poisson-disk, for improved image quality. This method, once optimized, can provide whole brain perfusion images in 2 minutes.Acknowledgements
No acknowledgement found.References
[1] Detre JA, et al. MRM 1992;23:37–45.
[2] Candes EJ, et al. IEEE TIT 2006;52:489–509.
[3] Donoho DL. IEEE TIT 2006;52:1289–1306.
[4] Lustig M, et al. MRM 2007;58:1182–1195.
[5] Zhou Y, et al. ISMRM 2013;pp.605.
[6] Zhao L, et al. Neuroimage. 2015;121:205–16.
[7] She H, et al. MRM 2014;71:645–660.
Figures