1412
A Novel Hybrid Total Variation Minimization Method to MRI Reconstruction from Highly Undersampled Data1Department of Biomedical Engineering, Department of Electrical Engineering, The State University of New York at Buffalo, Buffalo, NY, United States, 2School of Electronic Engineering, Xidian University, Xi'an, People's Republic of China, 3Institute of Biomedical and Health Engineering, Shenzhen Institutes of Advanced Technology, Shenzhen, People's Republic of China
Synopsis
This abstract presents a novel hybrid total variation minimization algorithm to reconstruct MR images from reduced measurements. The method combines the benefits of both L1 and homotopic L0 minimization algorithms for sparse signal reconstruction in the sense that substantially fewer measurements are needed for exact reconstruction. The algorithm minimizes the conventional total variation when the gradient is small, and minimizes the L0 of gradient when the gradient is large. An auto-adaptive threshold determines the transition between L1 and L0 of the gradients. The experimental results show the proposed algorithm outperforms either L1 or homotopic L0 minimization when the same reduction factor is used.
Purpose
Compressed sensing (CS) has been successfully applied in MRI to acquire and reconstruct sparse signals below the Nyquist rate. Both L1 minimization1 and homotopic L0 minimization2 algorithms have shown good results using reduced k-space data in compressed sensing MRI reconstruction. For images, L1 minimization algorithm of the signal is known to usually shrink the magnitude of reconstructions1,3. To address this issue, homotopic L0 minimization is proposed to replace L1 penalty by non-convex penalty3. However, the homotopic L0 minimization may suffer from local minimum resulting in lack of robustness when the signal is not strictly sparse or contaminated by noise4. In addition, there are several parameters to tune in order to get the optimal reconstruction. It is desirable to have the benefit of both methods.Theory and Methods
The proposed method is formulated as solving the following optimization problem: $$\min_{x}HTV(x) \;\;s.t.\;\;{\Phi}x=y,\quad(1)$$ where $$${\Phi}$$$ is the Fourier encoding matrix for reduced sampling, and y is the undersampled k-space data, and HTV is defined as $$HTX(x)=\,||x||_{HTV}\,={\sum_{ij}}\,f(\nabla_{i,j}\,x),\quad(2)$$ where $$ f(u)=\begin{cases}a|u|/\tau & |u| < \tau\\\frac{||u|-b|}{||u|-b|+\varepsilon} & |u| \geq \tau\end{cases}.\quad(3)$$ Constants $$$a=\frac{\sqrt{\varepsilon^{2}+4\tau\varepsilon}-\varepsilon}{\sqrt{\varepsilon^{2}+4\tau\varepsilon}+\varepsilon}$$$ and $$$b=\tau-\frac{\sqrt{\varepsilon^{2}+4\tau\varepsilon}-\varepsilon}{2}$$$ are chosen to make the function continuous and differentiable at $$$|u|=\tau$$$. In our earlier work on hybrid L0-L1 minimization5,6, we chose the corner of sorted magnitude of data as the threshold. Here we present a new method to automatically and iteratively update the threshold without manual tuning. The iteration starts with τ = 1, and then gradually reduces the value of τ with an exponential decay. The updating procedure continues until the tolerance and/or maximum iteration conditions are met.
Results and Discussion
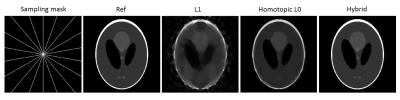
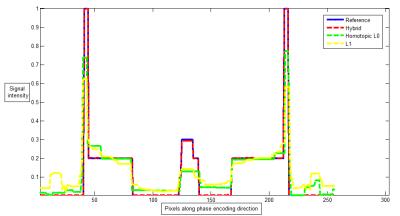
To evaluate the performance of the proposed method, we first use a 256 × 256 Shepp–Logan phantom to simulate the reduced acquisition with only 9 radial sampling spokes in k-space. Figure 1 shows the sampling mask, the reference image, and the reconstruction results using three competing algorithms. The effective reduction factor is 28.44. Figure 2 shows the reconstructed signal intensity using three competing algorithms (L1 and homotopic L0 minimization). It is seen that the hybrid minimization algorithm outperforms the other two algorithms. It suggests the proposed algorithm is more capable of reconstructing highly undersampled data.
The proposed method was also tested on a set of in vivo brain data. The data were acquired using a spin echo (SE) sequence (TR = 500 ms, matrix size = 256 × 256, FOV = 240 mm2) from a 3T MRI scanner (GE Healthcare, Waukesha, WI). A 2D variable-density random sampling pattern was used to undersample the k-space with a reduction factor of 5. Figure 3 shows the reference image, the reconstructed results using three competing algorithms and the corresponding zoomed region-of-interest. It is seen that there is over-smoothing artifact in L1 method and blocky artifact in homotopic L0 method. It suggests the proposed algorithm outperforms the other two algorithms in artifact suppression.
Conclusion
A novel hybrid total variation minimization algorithm with adaptive thresholding is proposed for compressed-sensing MRI reconstruction. The results show that the proposed algorithm can outperform the L1 and homotopic L0 minimization algorithms in reconstructing from highly undersampled k-space data.Acknowledgements
The work is supported in part by NSF CCF-1514403 and NIH R21EB020861. The authors would like to thank Dr. Joshua Trzasko for the homotopic L0 code and for his helpful discussion.
References
[1] Lustig, Michael, David Donoho, and John M. Pauly. "Sparse MRI: The application of compressed sensing for rapid MR imaging." Magnetic resonance in medicine 58.6 (2007): 1182-1195.
[2] Trzasko, Joshua, and Armando Manduca. "Highly undersampled magnetic resonance image reconstruction via homotopic-minimization." IEEE Transactions on Medical imaging 28.1 (2009): 106-121.
[3] Gasso, Gilles, Alain Rakotomamonjy, and Stéphane Canu. "Recovering sparse signals with a certain family of nonconvex penalties and DC programming." IEEE Transactions on Signal Processing 57.12 (2009): 4686-4698.
[4] Chartrand, Rick. "Exact reconstruction of sparse signals via nonconvex minimization." IEEE Signal Processing Letters 14.10 (2007): 707-710.
[5] Wang, Yong, et al. "A hybrid total-variation minimization approach to compressed sensing." 2012 9th IEEE International Symposium on Biomedical Imaging (ISBI). IEEE, 2012.
[6] Liang, D., and L. Ying. "A hybrid L0-L1 minimization algorithm for compressed sensing MRI." Proceedings of International Society of Magnetic Resonance in Medicine Scientific Meeting. 2010.
Figures