Synopsis

This abstract presents a novel method for compressed sensing (CS) MRI. This method combines the variable density random undersampling and iterative image reconstruction in CS-MRI with the regularly reduced bunched phase encoding (BPE) and linear equation based image reconstruction of BPE-MRI to further reduce data acquisition time and improve image quality of CS-MRI. Simulation results demonstrate the effectiveness and advantage of the presented method.

Introduction

Method

The proposed method uses BPE generated by zigzag variation of phase direction gradient and oversampling of k-space data during readout. Coupled with LEB reconstruction, BPE allows a regular reduction of factor R₁ > 1 along phase direction. LEB reconstruction² computes the image M using D = CM, where C is a Fourier coefficient matrix constructed based on the sample coordinates, and D is the bunched-sample matrix of k-space data acquired by BPE. The rows of D are in phase direction with dimension reduced by the factor R₁ and consist of the aliased data resulting from 1D IFFT along the rows. LEB reconstruction can produce aliasing free image from the data of single receive coil without using coil sensitivity map. Besides BPE, the proposed method uses an additional VD undersampling to randomly omit the regularly reduced BPEs by a factor R₂ > 1. This amounts to randomly undersampling the columns of D by the factor R₂ to acquire a subset of D, D_S = DE, using the undersampling matrix E. The D_S thus acquired is then used in the iterative CS reconstruction $$$argmin_\hat{D}\{||D_S-\hat{D}E||^2_{l_2}+\lambda_1||\Psi \hat{D}||_{l_1}+\lambda_2\|\hat{D}\|_{TV}\}$$$ to reconstruct the data matrix $$$\hat{D}$$$, which is in turn used in $$$\hat{D}$$$ = CM to reconstruct the image M. The above method is illustrated in Fig 1, which shows D_S is the physically acquired data with overall reduction R = R₁R₂.

We conducted simulation with in-vivo data to verify the proposed method. 2D spin-echo brain scan of a healthy volunteer was performed on 3T Skyra (Siemens HealthCare, Erlangen, Germany) using a 32-channel head coil (FOV: 240mm, Flip angle: 10^o, image matrix: 256 x 256) and only one channel’s data were used in simulation. Informed consent was taken in accordance with the institution’s ethics policy. The original 256x256 k-space data were interpolated to a 512 x 512 matrix, with the added data points simulating the data points of underlying continuous k-space within the original sampling grid. The interpolated data matrix were zigzag-sampled, with R₁ = 2, r = 2 (confer Fig 1), and then VD-undersampled along rows by the factor R₂ = 2 to obtain a 64x256 data matrix. This 64x256 data matrix simulates the physically acquired data with total reduction R = R₁R₂ = 4. It is used to form D_S for the iterative CS reconstruction to compute $$$\hat{D}$$$, which is used in $$$\hat{D}$$$ = CM to reconstruct the image M. For comparison, we also used VD-CS and FFT2 to reconstruct the images from the original k-space data.

Results

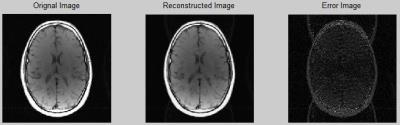
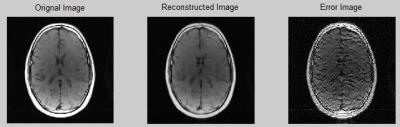
Fig 2 and Fig 3 compare the performance of the proposed method and VD-CS method at reduction R = 4. The reconstructed images and difference images of both methods clearly show the superiority of the proposed method over VD-CS method. Quantitatively, the relative error for the proposed method is 0.0914, whereas it is 0.2170 for VD-CS method.

Discussion

We have not compared the proposed method with the BPE alone method, because the latter has been reported to perform poorly at R = 4.²

Conclusion

Acknowledgements

References

1. Lustig M, Donoho DL, Santos JM, Pauly JM. Compressed Sensing MRI. IEEE Signal Processing Magazine. 2008;25(2):72-82.

2. Moriguchi H, Duerk JL. Bunched phase encoding (BPE): A new fast data acquisition method in MRI. Magnetic Resonance in Medicine. 2006;55(3):633-48.