Purpose

It is very important to reduce scan time of MRI. we hope to get fewer measurements for fast acquisition. However, insufficient sampling acquisition can degrade image quality and it leads to aliasing artifact because we cannot meet the Nyquist sapling ratio. Compressed Sensing (CS) ¹ is to reconstruct full-sampling like images from undersampled and aliased image. CS uses the sparsity of MRI in sparsifying transform such as wavelet domain and reconstructs the undersampled MR images into full-sampled-like image which do not have aliasing artifact. To solve the minimization problem of CS, choosing the proper regularization parameter is necessary. However, conventional setting of regularization parameter is manually selected in various experiments or to use the L-curve based setting which has some limitations (e.g. the smooth solution and the problem size) ². In order to overcome the limitation of L-curve method, this abstract proposes choosing the proper regularization parameter using no-reference image quality assessment (NR-IQA) not to have ground-truth images.

Methods

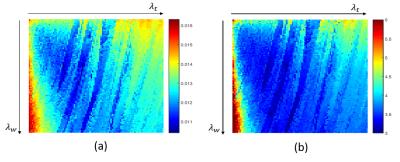
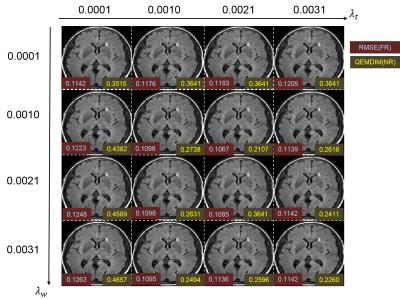
The way to reduce the artifact from the undersampled MR data is solving the optimization problem. The target image $$$x$$$ is acquired by minimizing the difference between the Fourier transform of target image $$$x$$$ and the undersampled real MR scan data y, which is used in 'data consistency'. The problem is made up by adding two terms of reducing artifacts, one is sparsity term in wavelet domain and another is total variance term. We need to set the weighting parameters , (which are called regularization parameters) on two terms of reducing artifacts. The solution of the optimization problem (1) is the target image which has data consistency with $$$y$$$ and its artifacts were minimized. The reconstructed image is varying with the regularization parameters. Setting the regularization parameters exploits the image quality assessment (IQA) of target image $$$x$$$. $$\min_{x}\parallel{F_{u}x-y}\parallel_{2}+\lambda_{w}\parallel{\Psi{x}}\parallel_{1}+\lambda_{t}TV_{x}\space\space\space\space(1)$$ Aliasing artifacts have directional structure. NIQE has possibility to detect aliasing artifact.³ but multi-directional filter so as to evaluate the structural information of image ⁴. Therefore, Quality evaluation using Multi Directional filters for MR images (QEMDIM) is good at evaluating image which has undersampled artifacts and highly correlated with Full Reference (FR)-IQA (e.g. RMSE, SSIM). (Figure 1). Reconstructed Images which the regularization parameters were set manually are evaluated using QEMDIM. The best quality image which has the lowest Q and its regularization parameters are selected. $$Q=\sqrt{(P_{r}-P_{e})^{T}(P_{r}-P_{e})}\space\space\space\space(2)$$ where $$$P_{r}$$$ and $$$P_{e}$$$ are the quality-aware features of the undistorted databases and distorted image. Since QEMDIM is no-reference IQA metric, reconstructed image can be directly evaluated. Therefore, the best quality images and the parameters can be obtained by repeating IQA process in various regularization parameters. Figure 1 shows that QEMDIM of CS results in various regularization parameters has high correlation with FR-IQA, RMSE. From this result, QEMDIM is great NR-IQA for in vivo CS reconstructed images. Figure 2 shows the process of parameter selecting using NR-IQA. Figure 3 shows that reconstructed images of reduction factor 2 images of 256X256 T2-FLIAR (Cartesian undersampling). Image quality results are various depending on regularization parameters. The trend of QEMDIM is similar to RMSE. From proposed method, we can know which the parameters are the most suitable to CS reconstruction.

Conclusion

Selecting the regularization parameters is very important in MRI reconstruction from undersampled k-space data. We proposed choosing optimized regularization parameters using IQA. The reconstructed image quality from proposed method is better than the conventional solution using the manual parameter. Furthermore, proposed method has great potential in MRI reconstruction. It is feasible to solve the limitation of choosing regularization parameters using L-curve based method. It also has potential to solve the optimization solution faster and more accurate by using IQA in iterative steps. It is meaningful to study on tuning of regularization parameter in CS using No Reference IQA.

Acknowledgements

This research was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIP) (2016R1A2R4015016).