Purpose

Compressed sensing (CS) methods that recover a discrete image from its discrete Fourier coefficients have revolutionized MR image acquisition and reconstruction. Recent continuous domain formulations^1-5 which directly recover the continuous signal or its Fourier coefficients are emerging as very attractive alternatives to discrete CS schemes. In addition to minimizing discretization errors, these algorithms also enable the exploitation of image structure (e.g. smooth connected edges)^3,4 which discrete compressed sensing strategies fail to fully exploit. The focus of this abstract is to develop a computationally efficient CD-CS framework and to investigate its utility in the recovery of dynamic MRI data.

Methods

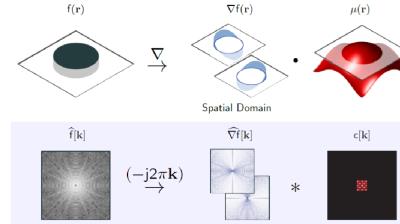
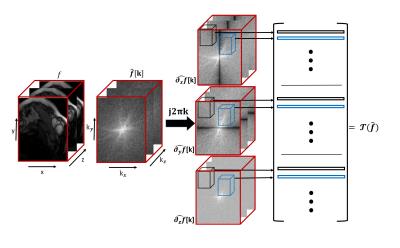
We assume the spatio-temporal volume $$$f$$$ to be a piecewise smooth function, whose gradients are non-zero only at locations specified by $$$\mu(\mathbf r)=0$$$ (zero level sets of $$$\mu$$$). We assume $$$\mu$$$ to be the inverse Fourier transform of a FIR filter $$$c[\mathbf k]; \mathbf k\in \Lambda$$$ supported on the cube-shaped support-set $$$\Lambda$$$. This implies that $$\nabla f(\mathbf r) \cdot \mu(\mathbf r) = 0;~~ \forall \mathbf r$$ An example of such an $$$f$$$ and the corresponding $$$\mu$$$ in 2-D are shown in figure (1). Note that the locations where $$$\mu=0$$$ are constrained by $$$\Lambda$$$. A low bandwidth implies that the non-zero locations of $$$\nabla f$$$ are localized to smooth curves, while a very high $$$\Lambda$$$ allows $$$\nabla f$$$ to be non-zero at arbitrary locations. Taking the Fourier transform of the above equation, we obtain the following k-space annihilation relation (see bottom row of Fig. 1): $$\widehat{\nabla f} \otimes c =0.$$ Rather than using the sparsity of the signal, we use the above annihilation relation to fill in the missing entries of $$$\hat f$$$ from its measurements. Specifically, we search for the filter $$$c$$$ with the smallest support that satisfies the data consistency. We observe that there is a one to one correspondence between the sparsity and bandwidth (size of $$$\Lambda$$$) in 1-D; current super-resolution methods may be viewed as special cases of the proposed formulation^1,2 The annihilation/convolution relations can be compactly represented in matrix form as $$\underbrace{\begin{bmatrix}\mathbf H(\widehat{\partial_x f})\\\mathbf H(\widehat{\partial_y f})\\\mathbf H(\widehat{\partial_t f})\end{bmatrix}}_{\mathbf{T}(\hat{f})} \mathbf c = \mathbf 0.$$ See figure (2) for an illustration of the matrix construction. The above annihilation relations imply that $$$\mathbf T(\hat{f})$$$ is low-rank^3,4. We exploit the low-rank property of the Toeplitz matrix to recover the dynamic MRI data from its undersampled multichannel measurements as: $${\hat{f}}^\star = \arg\min_{{\hat{f}}} \|\mathbf{T}(\hat{f})\|_p + \frac{\lambda}{2} \|\mathcal{A}(\mathbf F_t \hat{f}) - \mathbf{b}\|^2_2$$ where $$$\mathbf{b}$$$ represents the undersampled measurments, $$$\mathcal{A}$$$ is a linear operator representing sensitivity weighting, Fourier transform, and undersampling. $$$F_t$$$ is the inverse Fourier transform along the temporal dimension. We solve the above 3-D problem efficiently using the novel GIRAF algorithm⁶. While this framework has similarities to the recent work on structured low-rank problems in MRI⁵, the computational efficiency and lower memory footprint of the GIRAF algorithm enables us to use this framework for the first time on 3-D problems.

Results

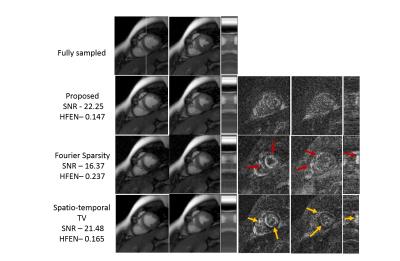
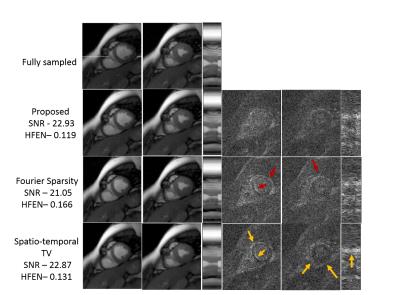
We demonstrate the algorithm on the recovery of a multi-channel breath-held CINE data of size 224x256x16 from 6% uniform random and 12 golden angle lines in figure (3) and figure (4) respectively. The dataset was acquired using a SSFP sequence using a five channel cardiac array with the following scan parameters: TE/TR = 2.0/4.1 ms, flip angle = 45$$$^{\circ}$$$, FOV = 350 mm². We compare the proposed method with spatio-temporal TV and temporal Fourier Sparsity regularized reconstruction methods. We observe that the reconstructions from the proposed approach are sharper and have fewer errors. As the proposed method exploits the smoothness of the edges, it results in improved reconstructions with fewer errors along the edges. (See captions for more details)

Conclusion

We introduced a novel continuous domain compressed sensing framework for the recovery of Dynamic MRI data from undersampled measurements. The matrix completion algorithm problem was solved using a computationally fast and memory efficient algorithm. Since the proposed approach exploited the edge information, it resulted in more accurate reconstructions with fewer errors along the edges.

Acknowledgements

No acknowledgement found.

References

1. Candès, Emmanuel J., and Carlos Fernandez-Granda. "Towards a Mathematical Theory of Super-resolution." Communications on Pure and Applied Mathematics 67.6 (2014): 906-956

2. Tang, Gongguo, et al. "Compressed sensing off the grid." IEEE Transactions on Information Theory 59.11 (2013): 7465-7490.

3. G.Ongie and M. Jacob, "Off-the-Grid Recovery of Piecewise Constant Images from Few Fourier Samples" SIAM J. Imaging Sci., 9(3), 1004–1041.

4. Ongie, Greg, and Mathews Jacob. "Super-resolution MRI using finite rate of innovation curves." 2015 IEEE 12th International Symposium on Biomedical Imaging (ISBI). IEEE, 2015.

5. Kyong Hwan Jin, Dongwook Lee, Jong Chul Ye, "A general framework for compressed sensing and parallel MRI using annihilating filter based low-rank Hankel matrix", arXiv:1504.00532.

6. Greg Ongie, Mathews Jacob, "GIRAF: A Fast Algorithm for Structured Low-Rank Matrix Recovery", arXiv:1609.07429.