1405
Background Field Removal Technique using Non-regularized Variable Kernels Sophisticated Harmonic Artifact Reduction for Phase Data for Quantitative Susceptibility Mapping1Department of Radiology, Nagoya City University Hospital, Nagoya, Japan, 2Unit of Healthcare Business, Hitachi, Ltd.
Synopsis
QSM
is relatively new biochemical and quantitative reconstruction method which
directly estimates the iron distribution. It needs a precision of separation of
local field from background field for measurement of accurate susceptibility
value. We introduced a novel method using non-regularized variable kernels
sophisticated harmonic artifact reduction for phase data (NR-VSHARP). The proposed
method utilized multiple kernel sizes and minimization of norm only inside mask
without any regularization parameter. NR-VSHARP enabled to estimate high accurate local field, compared with VSHARP. NR-VSHARP method provides high accurate local field map with saving cortical information.
PURPOSE
Quantitative susceptibility mapping (QSM) is recently developed post-processing which directly estimates the iron overload in the brain. The post-processing steps for QSM are phase unwrapping, background field removal, and dipole inversion. It is important to separate local field from background field caused by inhomogeneity of static magnetic field in evaluating an accurate susceptibility value in QSM. Variable kernels sophisticated harmonic artifact reduction for phase data (VSHARP) was reported by Wei, et al1. VSHARP utilizes the multiple spherical mean value (SMV) kernels and threshold for truncated singular value decomposition (TSVD) to minimize the loss of cortical phase information while mitigating phase artifacts. It succeeded in producing minimal boundary loss and lower phase error. However, it needs to predefine a threshold for TSVD. In this abstract, we introduced a non-regularized VSHARP (NR-VSHARP) which allowed to separate the background field without a predefined regularization parameter.METHODS
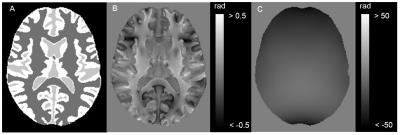
Numerical brain phantom: 1 mm3 isotropic numerical brain phantom was generated from MNI152 T1 weighted structural template imaging segmented into four tissue types with following susceptibilities (white matter, 0.03 ppm; gray matter, -0.02 ppm; cerebral spinal fluid, 0 ppm; air, 9 ppm)2. The brain phantom was convolved with the dipole kernel to generate the total field map (Fig. 1). The true local field was obtained from the phantom with 0 ppm background susceptibility source in a manner similar to the aforementioned method.
Brain imaging: Human brain experiment was conducted on a healthy volunteer using TRILLIUM OVAL 3.0 T scanner (Hitachi, Tokyo, Japan). The phase images were obtained using 1 mm3 isotropic flow compensated 3D spoiled gradient echo sequence with following parameters: FOV = 192 x 192 x 140 mm3, TE = 25 ms, TR = 40 ms, flip angle = 20 degrees. The unwrapped total field map was obtained from original wrapped images using Laplacian-based phase unwrapping3.
Data analysis: The proposed NR-VSHARP was a method for separating local tissue field from background field caused by static magnetic inhomogeneity without any regularization. The proposed method used variable SMV kernel sizes and minimized a L2 norm only inside the brain mask. The SMV kernel sizes were gradually reduced toward the boundary of brain mask for minimizing the erosion of brain mask induced by SMV filtering. The minimization of L2 norm was restricted to only the part of the brain mask to eliminate any phase information in extended region close to boundary. The estimated local field was obtained from the following minimization:
$$min_{B_L∈M_{minimum radius}}\parallel\sum S_{inv}M_iF^{-1}S_iF(B_T-B_L)\parallel_2^2$$
where Sinv is inverse SMV kernel of largest kernel size with 0.1 TSVD threshold for rapid convergence, Mminimum radius is mask eroded the diameter of smallest SMV kernel size, Mi is binary mask eroded the diameter of used SMV kernel size, Si is variable SMV kernels, and BT and BL are total and local field. The local field estimated by VSHARP method was calculated from the following equation:
$$B_L=F^{-1}S_{inv}\sum F(M_iF^{-1}S_iFB_T) $$
We compared the relative errors in NR-VSHARP and VSHARP with 0.03 threshold for TSVD to evaluate the accuracy of each method in numerical brain phantom and human brain experiment.
RESULTS AND DISCUSSION
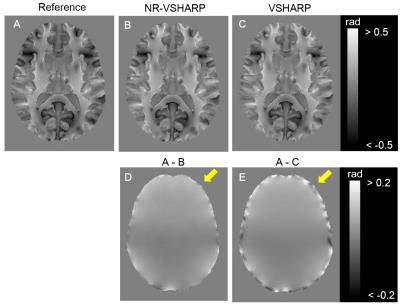
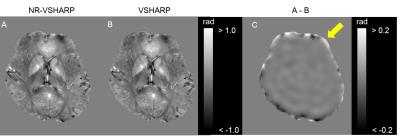
The relative errors in whole numerical phantom were 33.0 % and 38.4 % in NR-VSHARP and VSHARP, respectively (Fig. 2). NR-VSHARP method enabled to minimize a loss of phase information in boundary region and to estimate more accurate local field without any regularization, due to the minimization of L2 norm only inside brain mask iteratively. The relative errors in boundary applied smaller kernel sizes were 22.2 % and 24.4 % in NR-VSHARP and VSHARP, respectively. There was no clear difference between NR-VSHARP and VSHARP in the region far from boundary. In contrast, the relative errors in the boundary applied smaller SMV kernel sizes were 51.2 % and 61.0 % in NR-VSHARP and VSHARP, respectively (Fig. 2D and E). The VSHARP’s error in the boundary region was caused by mismatch of the used SMV kernel sizes in convolution and deconvolution processes2, 4. In human experiment, NR-VSHARP method enabled to suppress large phase offset in the region close to boundary and estimated more accurate phase value (Fig. 3).CONCLUSION
NR-VSHARP is simple background field removal to provide the minimal loss of boundary and high precision of phase data. This technique may help to achieve better accuracy of QSM.Acknowledgements
No acknowledgement found.References
(1) Wu B, et al. Magn Reson Med: 67(1); 137-147 (2012)
(2) Kan H, et al. Magn Reson Imaging: 34; 1026-1033 (2016)
(3) Bagher-Ebadian H, et al. J Magn Reson Imaging: 27; 649-652 (2008)
(4) Schweser F, et al. NMR Biomed: in press (2016)
Figures