1389
Susceptibility-induced local ΔB0 variations are essential for predicting EPI distortions in the breast1Center for Image Sciences, UMC Utrecht, Utrecht, Netherlands, 2Department of Biomedical Engineering, Eindhoven University of Technology, Eindhoven, Netherlands
Synopsis
Applications involving EPI readouts, such as diffusion weighted imaging and functional imaging, are hampered by geometrical distortions caused by static field inhomogeneities (ΔB0). Pixel shift maps can be inferred from ΔB0 maps. Though it is common practice to smooth these maps before calculating pixel shifts, doing so reduces susceptibility-induced local ΔB0 variations. This study investigates the importance of local ΔB0 changes in correctly predicting EPI distortions. Preliminary data obtained from the human breast in-vivo shows that susceptibility-induced changes in ΔB0 are essential in accurately predicting EPI distortions.
Purpose
Echo planar imaging (EPI) is currently the most common acceleration technique when performing diffusion weighted (DWI) or functional imaging (fMRI). Images recorded using EPI readouts are prone to several artefacts, most prominently geometrical distortions caused by static field inhomogeneities (ΔB0). Several correction methods are available that attempt to recover undistorted images, both retrospectively and prospectively.1 When applying retrospective correction using ΔB0 maps, whether estimated from a multi-echo acquisition or from a reversed phase-encoded EPI acquisition, it is common practice to ensure these maps are smooth by e.g. low-pass filtering, polynomial fitting or kernel smoothing. This practice eliminates noise from ΔB0 maps, since noise can give rise to inconsistencies in the inferred displacement fields. It also reduces local ΔB0 variations induced by susceptibility differences at tissue interfaces. This study investigates the role of susceptibility-induced local variations in ΔB0 maps in the prediction, and ultimately correction, of EPI distortions.Methods
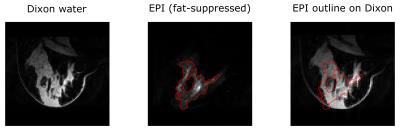
A healthy female volunteer (aged 27 years) underwent a breast MRI examination using a unilateral breast coil setup on a 7T whole-body MR system (Achieva; Philips, Cleveland, Ohio, USA). The protocol involved a gradient-echo Dixon acquisition (1.5x1.5x1.5 mm3), a fat-suppressed spin-echo EPI (2x2x3 mm3, bandwidth/voxel 20 Hz) and a dual-echo ΔB0 measurement (2.5x2.5x2.5 mm3). In order to study global and local ΔB0 effects separately, the global ΔB0 variation was determined by performing a 3rd-order polynomial fit to the measured map, while the local variation was inferred from the Dixon acquisition. Based on the Dixon in-phase, water and fat reconstructions, a 3D susceptibility model of the volunteer’s breast was constructed, using tabulated values for air, water and fat.2, 3 From this model, local ΔB0 variation can be predicted.4 For each of the maps (fitted global ΔB0, measured ΔB0, and the fitted global + modelled local ΔB0) we simulated the EPI distortions on the water reconstruction of the Dixon acquisition. The simulation was performed with the FORECAST method, restricted to only simulating distortions in the phase encoding direction (EPI direction).5 We compared each of the simulated EPI images with the measured EPI acquisition, both visually and quantitatively using the Pearson correlation coefficient (CC), to assess the importance of local ΔB0 variations.Results
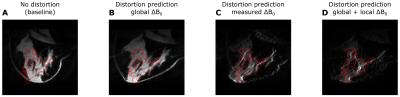
Figure 1 shows the original Dixon water reconstruction and the EPI image in the same slice. Note that, in the EPI image, the deformation causes the glandular tissue to appear as sheared and substantially compressed with respect to the undistorted image. Figure 2 shows the composition of the breast model that was used to simulate local susceptibility-induced ΔB0 effects. The right panel indicates that local changes at tissue boundaries can be substantial, especially compared to the global gradient caused by the tissue-air boundary. Figure 3 shows the simulated EPI images for global, measured, and global + local ΔB0 distributions respectively, with the measured EPI’s outline overlaid. Table 1 reports the CC as a quantitative metric for distortion prediction accuracy.Discussion
The results in Figure 3 demonstrate that it is not sufficient to use global ΔB0 variation to predict EPI distortions. Adding local susceptibility-induced effects seems to aid substantially in achieving a better prediction of the distortion; note the high agreement between the measured EPI’s outline and the simulated image in panel d of Figure 3, and the increased CC in Table 1. Whether inclusion of a model of susceptibility-induced ΔB0 effects improves EPI distortion prediction with respect to using measured ΔB0 maps should be confirmed in a larger in vivo study.
We are aware of the fact that it is questionable whether it is desired or even feasible to acquire ΔB0 maps at a sufficiently high resolution to capture local effects in a clinical setting, since they require long scan times and tend to be noisy. However, deriving local ΔB0 information from anatomical scans already present in clinical protocols is generally achievable, e.g. by using susceptibility models derived from anatomical scans as we've done here.
Though this study focusses on prediction of EPI distortion, we feel our results are relevant when designing distortion correction techniques. As we show local ΔB0 information is required to obtain reliable predictions, correction techniques will most likely improve from incorporating this information. For accurate distortion correction in EPI breast imaging, this would mean that including local ΔB0 variation induced by the susceptibility differences between fat and parenchymal tissue, will be essential.
Conclusion
Preliminary work shows that smoothing ΔB0 maps prior to using them for EPI distortion correction can lead to substantial underestimation of the deformation. Including local susceptibility-induced ΔB0 variation, inferred from anatomical scans, will improve distortion correction algorithms.Acknowledgements
This work is part of the IMDI research program with project number 104003019, which is (partly) financed by the Netherlands Organization for Scientific Research (NWO).References
1. Hancu I, Lee S K, Hulsey K, et al. Distortion correction in diffusion-weighted imaging of the breast: Performance assessment of prospective, retrospective, and combined (prospective + retrospective) approaches. Magn Reson Med. 2016;early view.
2. Hopkins J A, and Wehrli F W. Magnetic susceptibility measurement of insoluble solids by NMR: Magnetic susceptibility of bone. Magn Reson Med. 1997;37(4):494-500.
3. Schenck J F. The role of magnetic susceptibility in magnetic resonance imaging: MRI magnetic compatibility of the first and second kinds. Med Phys. 1996;23(6):815-850.
4. Bouwman J G, and Bakker C J G. Alias subtraction more efficient than conventional zero-padding in the Fourier-based calculation of the susceptibility induced perturbation of the magnetic field in MR. Magn Reson Med. 2012;68(2):621-630.
5. Zijlstra F, Bouwman J G, Braškute I, et al. Fast Fourier-based simulation of off-resonance artifacts in steady-state gradient echo MRI applied to metal object localization. Magn Reson Med. 2016;in press.
Figures