1382
Stacked Frequency Wave Inversion (SFWI): Heterogeneous And Edge-Preserving Direct Inversion For Magnetic Resonance Elastography (MRE)1Radiological Science, Charité Universitätsmedizin Berlin, Berlin, Germany, 2Physics, Indian Institute of Technology Delhi, New Delhi, India, 3Medical Informatics, Charité Universitätsmedizin Berlin, Berlin, Germany
Synopsis
A new reconstruction method for MR elastography exploits a recent finding of mathematical uniqueness to develop a heterogeneity-accommodating and edge-preserving direct inversion method that uses first order derivatives. We investigate this new method on FEM models and a cohort of in vivo brain acquisitions by comparing it with a previously published method known as ESP. In models the method removes artefacts from use of second derivatives and homogeneity assumptions. In brain images appear better conditioned, but shows values differing from ESP in more anisotropic brain regionss.
Introduction
Magnetic Resonance Elastography (MRE) [1] recovers estimates of the shear modulus of soft tissue using phase-contrast MR imaging. MRE produces 4d vectorial fields of steady-state shear wave displacements over time. After temporal Fourier transform and removal of the divergence component of the field with a Hodge decomposition [2], the displacement form of the steady state Navier-Lamé wave equation for isotropic viscoelastic materials reads:
$$(\mu(u_{i,j} + u_{j,i}), j = -\rho\omega^{2}u~~(1)$$
where $$$\mu$$$ is the shear modulus, $$$u$$$ is the curl field, $$$\rho$$$ is tissue density and $$$\omega$$$ the frequency of vibration. This equation contains three observation vectors (the x, y, and z displacements) but four unknowns ($$$\mu$$$ and its three directional derivatives). Hence estimation of $$$\mu$$$ off a single acquisition requires additional conditioning of the problem to obtain a uniqueness condition for the solution, such as the estimation of boundary conditions for $$$\mu$$$ (e.g. [3, 4]) or the enforcement of local homogeneity and by extension Sommerfield boundaries [5]. However, recently Sanchez et al. [6] showed that the uniqueness condition of Eq. 1 could be met by "stacking" two or more linearly decorrelated acquisitions into a single recovery. Such fusion of multiple decorrelated acquisitions has precedent in the MDEV inversion approach [7], which combines wave acquisitions at multiple driving frequencies; however MDEV assumes local homogeneity and uses second order derivatives.
Methods
Here we introduce Stacked Frequency Wave Inversion (SFWI), which combines the above findings with image processing developed in [8] to accomplish several recovery goals at once. In SFWI, displacements are obtained across a narrow band of frequencies (here 20, 25, and 30 Hz) to generate decorrelated shear wave acquisitions with minimal impact of frequency dispersion. Curl fields are obtained using a nonlinear least-squares Helmholtz-Hodge decomposition [9]. Denoising and differentiation are then performed in the complex wavelet domain [8]. Finally, $$$\mu$$$ is solved for in heterogeneous form as described in Eq. 1 using overdetermined least squares (LSQR method [10]). For validation SFWI was compared against the MDEV-based ESP pipeline [8] using FEM model data acquisitions similar to those in [9]; caliper wavelength measurements of the simulation produced ground truths of 1600 Pa for soft target, 6600 Pa for hard target, and 3200 Pa for background, respectively. Then, for a pilot in vivo investigation, inter-and intra-subject whole-brain results were evaluated in brain MRE, by using the SFWI and ESP techniques on four subjects scanned three times each using the method in [11]. Whole brain means were obtained by averaging all values in the image above 300 Pa, a value calculated to be more than two standard deviations above noise values in the image, but more than two standard deviations below tissue results.Results
Results for the FEM simulation are in Figure 1. For background, hard target and soft target, SFWI measured 1498, 3271, and 6674 Pa while ESP measured 1623, 3124 and 7505 Pa. Inspection shows that the ESP simulation distorts the shape of the targets by a ring of artefactual pixels around the boundary, and by a visible gradient through the targets, while SFWI shows none of these artifacts.
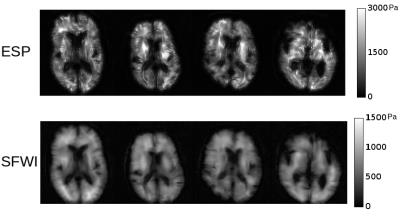
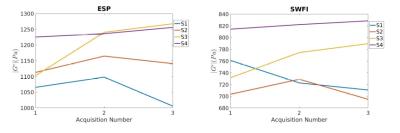
For the brain cohort, exemplar slices from the first scan of each subject, processed with ESP and SFWI, are shown in Figure 2 and a results table is given in Figure 3 containing whole-brain means for four subjects scanned three times.
Discussion
In the FEM simulations, SFWI shows values similar to ESP, however all prominent artifacts in the ESP image mentioned above are not present. Further, the higher de-noising levels required for the use of second-order derivatives in ESP appear to have caused overestimation of the hard target.
In brain, SFWI stiffness estimates reach the full boundaries of the brain tissue, and within tissue regions the image is texturally smoother and more consistent. Whole-brain values for SFWI were lower than ESP, with a mean across all acquisitions of 767 Pa in SFWI vs 1151 in ESP. This discrepancy is principally from regions in the brain known to be more anisotropic which violates the isotropic model governing both reconstructions. These regions measure substantially stiffer in ESP, hence one likely explanation is that the use of second derivatives accentuates the sensitivity of the method to this violation of its assumptions. Overall SFWI values were in line with results in [11]. More sophisticated brain segmentation methods will likely reduce variance between scans.
In conclusion, SFWI combines many desired properties at once -- heterogeneity, preservation of edges, use of first order derivatives, and direct inversion -- while showing strong consistent results in models and promising initial results in brain tissue.
Acknowledgements
The authors acknowledge conversations with Dr. Penelope Davies, University of Strathclyde, and thank the University of Edinburgh for providing the finite element models.References
[1] Hirsch et al. (2016) Magnetic resonance elastography: physical background and medical applications, Wiley-VCH
[2] Sinkus et al. (2005) Imaging anisotropic and viscous properties of breast tissue by magnetic resonance-elastography, Mag Res Med 53:372–387
[3] Park & Maniatty (2006) Shear modulus reconstruction in dynamic elastography: time harmonic case, Phys. Med. Biol. 51 (2006) 3697–3721
[4] Van Houten et al. (1999) An overlapping subzone technique for MR-based elastic property reconstruction, Mag Res Med 42:779–786
[5] Papazoglou et al. (2008) Algebraic Helmholtz inversion in planar magnetic resonance elastography, Phys Med Biol 53:3147–3158
[6] Sanchez et al. (2010) Elastography of biological tissue: direct inversion methods that allow for local shear modulus variations, ICIAR 2010:195-206
[7] Papazoglou et al. (2012) Multifrequency inversion in magnetic resonance elastography, Phys Med Biol 57:2329–2346
[8] Barnhill et al. (2016) Nonlinear multiscale regularization in magnetic resonance elastography, Med Imag Anal 35:133–145
[9] Bahl & Senthilkumaran (2012) Helmholtz Hodge decomposition of scalar optical fields, J Opt Soc Am A 29(11):2421-2427
[10] Paige and Saunders, LSQR: An algorithm for sparse linear equations and sparse least squares, TOMS 8(1), 43-71 (1982).
[11] Dittmann et al. In vivo wideband multifrequency MR elastography of the human brain and liver, Mag Res Med 76:1116–1126
Figures