1378
Hadamard Encoding for Magnetic Resonance Elastography1Institute for Biomedical Engineering, University and ETH Zurich, Zurich, Switzerland, 2Division of Imaging Sciences and Biomedical Engineering, King's College London, London, United Kingdom, 3Department of Radiology, Academic Medical Center, Amsterdam, Netherlands
Synopsis
We propose the use of Hadamard encoding for Magnetic Resonance Elastography (MRE) of the full displacement vector field (4D-MRE). To this end, motion is encoded along the four diagonals of the regular cube spanned by the main gradient axes. This allows for a factor four higher phase accumulation compared to classical, unbalanced four-point encoding within the same acquisition time. In this abstract, we demonstrate the increase in phase-to-noise ratio for a gel phantom and show the direct benefit of using Hadamard encoding in-vivo to capture high-quality wave displacement maps in the brain.
Introduction
Magnetic Resonance Elastography allows the in-vivo determination of the local tissue shear stiffness by time-resolved measurement of the 3D displacement field induced by an external actuator1. Recent advances in the field have focused on the development of actuator systems2–5, wave inversion algorithms6–9, and improved acquisition techniques3,10–14, where the latter is mainly driven by the need to balance resolution, total scan duration, and achievable phase-to-noise ratio (PNR). Our focus in this work lies on the efficient encoding of motion and the correction of field-inhomogeneity induced phase errors. Current 4D MRE acquisitions typically utilize motion encoding in three orthogonal directions and either acquire a fourth reference scan without motion sensitization (unbalanced four-point scheme) or additionally acquire three encodings with inverted motion sensitizing gradient3,15,16. In the former case, a common reference scan leads to correlated noise between the motion directions, while the latter method has uncorrelated noise and benefits from doubled motion sensitivity at the cost of a 50% longer scan duration relative to four-point encoding17. In this work, we incorporate Hadamard encoding in a standard fractional gradient-echo based MRE sequence leading to a four-fold increase in motion sensitivity and uncorrelated noise between different encoding directions without an increase in total scan duration compared to unbalanced four-point encoding.Theory
The signal phase $$$\varphi_{t_0}$$$ in each voxel can be written as a superposition of four phase components $$\vec{\phi}_{t_0}:=\begin{pmatrix}\phi_{t_0,x}&\phi_{t_0,y}&\phi_{t_0,z}&\phi_{B_0}\end{pmatrix}^\text{T},$$where $$$\phi_{t_0,i}$$$ denotes the motion induced phase along the i-th coordinate axes and $$$\phi_{B_0}$$$ denotes the phase-offset caused by field inhomogeneities. A full 4D MRE data set then comprises multiple signal phases$$\vec{\varphi}=\hat{E}\cdot\vec{\phi},$$where $$$\hat{E}$$$ is the phase-encoding matrix, which is determined by the underlying phase encoding scheme. The shear motion induced phase along the primary axes $$$\phi_{t_0,i}$$$ is then retrieved through inversion of the above encoding equation $$\vec{\phi}=\text{pinv}\left(\hat{E}\right)\vec{\varphi},$$where $$$\text{pinv}$$$ denotes the pseudo inverse. The encoding matrices for unbalanced four-point (u4p) and Hadamard encoding (Had) are given by17 $$\hat{E}_{\text{u4p}}:=\begin{bmatrix}+1&0&0&+1\\0&+1&0&+1\\0&0&+1&+1\\0&0&0&+1\end{bmatrix}$$and$$\hat{E}_{\text{Had}}:=\begin{bmatrix}+1&+1&+1&+1\\+1&-1&-1&+1\\-1&+1&-1&+1\\-1&-1&+1&+1\end{bmatrix}.$$Hence, in Hadamard encoding motion is encoded along the non-orthogonal direction vectors of a regular tetrahedron, instead of encoding along the primary coordinate axes (Figure 1). Calculation of the pseudo-inverse of the encoding matrices shows that Hadamard encoding combines all four measurements thus leading to a four times higher encoding efficiency17.Methods
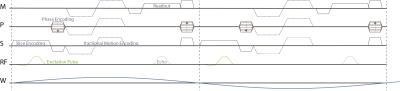
The proposed encoding scheme was implemented on a Philips Achieva 3T system and wave data were acquired in an ultrasound gel phantom and in the brain of two volunteers. All measurements were performed using the “eXpresso” sequence18, i.e. a spoiled gradient echo sequence (Figure 2) with fractional encoding19, a shear wave frequency of 30 Hz, two shots per wave cycle, and Cartesian readout. The wave propagation was captured eight times per wave cycle and the motion encoding gradient direction was varied according to the unbalanced four-point and Hadamard encoding scheme after a full set of phase contrast MRI images were acquired. Synchronization to the externally generated wave was achieved using a TTL trigger signal and the repetition time was set equal to the wave period. The full set of scan parameters is given in Table 1.Results and Discussion
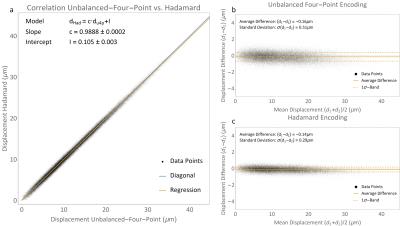
In Figure 3a, a correlation plot of unbalanced four-point and Hadamard encoding is displayed for the gel phantom, showing excellent correlation. In Figure 3b and c, Bland-Altman plots of the two methods are shown, clearly depicting the considerable reduction of displacement map noise for Hadamard encoding (0.29 μm vs. 0.51 μm for unbalanced four-point encoding). The theoretically achievable PNR is given by $$$\epsilon^{-1}_{\text{u4p}}\epsilon_{\text{Had}}/\sqrt{2}\approx2.3$$$, where $$$\epsilon$$$ denotes the encoding efficiencies of the two methods (see Table 1). The achieved PNR increase of 1.8 is lower as additional experimental noise contributions to PNR are not being taken into account in the above analysis.
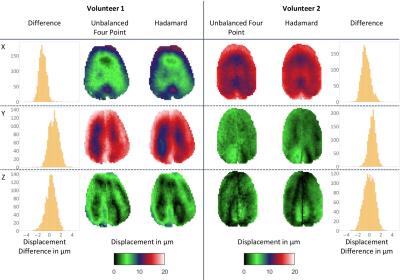
In Figure 4, displacement maps for one selected slice of the 3D in-vivo brain scans of two volunteers are presented for four-point and Hadamard encoding and all three motion encoding directions, which are in very good qualitative and quantitative agreement. Due to limited wave coupling of the mechanical actuator, only one propagation direction shows pronounced waves. Hadamard encoding allows for better visualization of displacement amplitudes in low-amplitude regions (black-to-green) and overall leads to a reduction of noise.
Conclusions
We have demonstrated the feasibility of Hadamard encoding for in-vivo MRE of the brain, resulting in a significant increase in PNR without increase in total scan duration or loss of resolution. This increase in encoding efficiency can be used to further increase PNR in already clinically feasible scans or to reduce acquisition time by higher fractional encoding, reduced number of acquired phase cycles, or to compensate for SNR loss caused by sub-Nyquist acquisition.Acknowledgements
This project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 668039.References
1. Muthupillai, R. et al. Magnetic resonance imaging of transverse acoustic strain waves. Magn. Reson. Med. 36, 266–274 (1996).
2. McGrath, D. M. et al. Evaluation of wave delivery methodology for brain MRE: Insights from computational simulations. Magn. Reson. Med. 0, (2016).
3. Anderson, A. T. et al. Observation of direction-dependent mechanical properties in the human brain with multi-excitation MR elastography. J. Mech. Behav. Biomed. Mater. 59, 538–546 (2016).
4. Fehlner, A. et al. Cerebral multifrequency MR elastography by remote excitation of intracranial shear waves. NMR Biomed. 28, 1426–1432 (2015).
5. Numano, T., Mizuhara, K., Hata, J., Washio, T. & Homma, K. A simple method for MR elastography: A gradient-echo type multi-echo sequence. Magn. Reson. Imaging 33, 31–37 (2015).
6. Honarvar, M., Rohling, R. & Salcudean, S. E. A comparison of direct and iterative finite element inversion techniques in dynamic elastography. Phys. Med. Biol. 61, 3026–3048 (2016).
7. Tzschätzsch, H., Guo, J., Dittmann, F., Braun, J. & Sack, I. in Bildverarbeitung für die Medizin 2006 p3–7 (Springer Berlin Heidelberg, 2016).
8. Honarvar, M., Lobo, J., Mohareri, O., Salcudean, S. E. & Rohling, R. Direct vibro-elastography FEM inversion in Cartesian and cylindrical coordinate systems without the local homogeneity assumption. Phys. Med. Biol. 60, 3847–3868 (2015).
9. Petrov, A. Y., Docherty, P. D., Sellier, M. & Chase, J. G. Multi-frequency inversion in Rayleigh damped Magnetic Resonance Elastography. Biomed. Signal Process. Control 13, 270–281 (2014).
10. Johnson, C. L. et al. Magnetic resonance elastography of the brain using multishot spiral readouts with self-navigated motion correction. Magn. Reson. Med. 70, 404–412 (2013).
11. Klatt, D., Yasar, T. K., Royston, T. J. & Magin, R. L. Sample interval modulation for the simultaneous acquisition of displacement vector data in magnetic resonance elastography: theory and application. Phys. Med. Biol. 58, 8663–75 (2013).
12. Klatt, D., Johnson, C. L. & Magin, R. L. Simultaneous, multidirectional acquisition of displacement fields in magnetic resonance elastography of the in vivo human brain. J. Magn. Reson. Imaging 42, 297–304 (2015).
13. Johnson, C. L. et al. 3D multislab, multishot acquisition for fast, whole-brain MR elastography with high signal-to-noise efficiency. Magn. Reson. Med. 71, 477–485 (2014).
14. Yasar, T. K., Klatt, D., Magin, R. L. & Royston, T. J. Selective spectral displacement projection for multifrequency MRE. Phys. Med. Biol. 58, 5771–81 (2013).
15. Yin, Z., Kearney, S. P., Magin, R. L. & Klatt, D. Concurrent 3D acquisition of diffusion tensor imaging and magnetic resonance elastography displacement data (DTI-MRE): Theory and in vivo application. Magn. Reson. Med. 0, (2016).
16. Sahebjavaher, R. S. et al. Prostate MR elastography with transperineal electromagnetic actuation and a fast fractionally encoded steady-state gradient echo sequence. NMR Biomed. 27, 784–794 (2014).
17. Pelc, N. J., Bernstein, M. A., Shimakawa, A. & Glover, G. H. Encoding strategies for three-direction phase-contrast MR imaging of flow. J. Magn. Reson. Imaging 1, 405–413 (1991).
18. Garteiser, P. et al. Rapid acquisition of multifrequency, multislice and multidirectional MR elastography data with a fractionally encoded gradient echo sequence. NMR Biomed. 26, 1326–1335 (2013).
19. Rump, J., Klatt, D., Braun, J., Warmuth, C. & Sack, I. Fractional encoding of harmonic motions in MR elastography. Magn. Reson. Med. 57, 388–395 (2007).
Figures