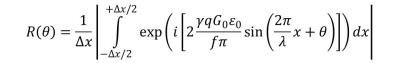1376
Introduction of IVPD-MRE: Quantitative Assessment of Shear Stiffness without Spatial Derivative Operators1Richard and Loan Hill Department of Bioengineering, University of Illinois at Chicago, Chicago, IL, United States
Synopsis
Intravoxel phase dispersion (IVPD) in MRE describes signal loss of the MR magnitude due to spin dephasing imposed by voxel deformation. The extensity of IVPD is, among other parameters, dependent on the tissue stiffness. Therefore, tissue stiffness can be quantified by analyzing IVPD-imposed signal loss within a single voxel. The new approach does not rely on the use of spatial derivative operators as in conventional MR Elastography. In the present work, we examine in simulations the extensity of IVPD for varying experimental conditions and present stiffness maps of an inhomogeneous phantom, which were calculated by numerically fitting the IVPD equation.
Target Audience
Scientists
and Engineers interested in Elastography.Purpose
MR Elastography (MRE) is a phase-contrast based MRI technique that is capable of measuring diagnostically relevant tissue stiffness.1 Conventionally, stiffness reconstruction algorithms require the application of second or third order spatial derivative operators to the measured MRI phase.2 Therefore, the effective spatial resolution of the stiffness maps is lower than the inherent MR image resolution and errors can occur when spatial differences of the MRI phase are calculated across tissue boundaries. The purpose of this work is the introduction of a new magnitude-contrast based MRI protocol for stiffness assessment that does not rely on the application of spatial differences. Our approach, that we name IVPD-MRE, is based on the intravoxel phase dispersion (IVPD) effect, which represents MRI signal reduction due to dephasing imposed by vibration induced voxel deformation. Stiffness assessment using magnitude data has been performed previously, but Glaser et al. analyzed spatial wave structure imposed by IVPD.3 In contrast our approach is capable of quantifying stiffness from single voxel information and has the potential to provide an effective resolution of the stiffness map that is equal to the inherent resolution of the MRI magnitude image.Methods
Conventionally in MRE, the interactions between oscillating gradients and vibrating magnetized tissue enable the encoding of the vibration phase into the phase of the macroscopical magnetization. However, the voxels also deform, which causes a dephasing of the magnetic moments within one voxel and subsequently this dephasing results in MR signal loss R. Yin et al.4 have derived R for the case of an elastic shear wave with wave normal along the x-direction, see figure 1 for eq. 1. Here λ, ε0 and f correspond to the length, amplitude and frequency of the shear wave. The vibration phase in voxel center, the gyromagnetic ratio, the voxel edge length and the cycle number and amplitude of the motion encoding gradient (MEG) are denoted with θ, γ, Δx, q and G0, respectively. We performed numerical forward simulations of eq. 1 to examine the extensity of IVPD induced signal loss in dependence of experimental parameters. In the experiments, we used an inhomogeneous agarose phantom with cylindrical symmetry consisting of a softer inner and stiffer outer part (0.5% vs. 1.0% agar in water). The cylindrical sample bin was mechanically excited along the axial direction with 500 Hz vibration frequency. Out-of-plane displacements were acquired in 16 time steps (equally shifted over the 2 ms vibration period) using a modified spin-echo sequence with 6 cycles of a sinusoidal MEG of 500 Hz vibration with 250 mT/m amplitude. Further relevant sequence parameters were: TR=1s, TE=17.1ms; field of view: 36mmx36mm with 0.5mm slice thickness. Two matrix sizes were used, 32x32 and 64x64, and two levels of the vibration amplifier, high and low. We replaced λ = c/f in eq. 1 and varied the shear wave velocity c from 0.1-10 m/s in increments of 0.1 m/s to fit eq. 1 to the measured signal reduction. Note, that the stiffness is proportional to c2 in an elastic model. All other parameters in eq. 1 are known except for ε0, which was taken from the phase image.
Results
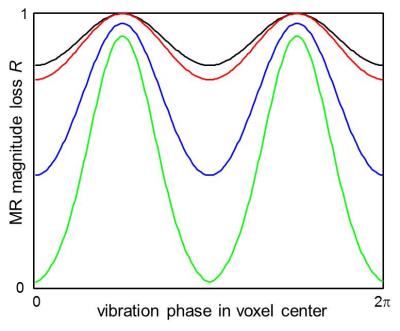
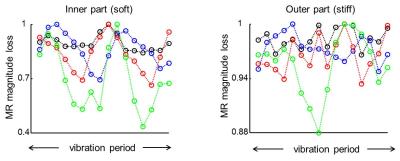
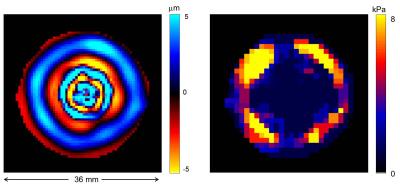
Figure 2 illustrates the IVPD effect under different experimental conditions. It is perceptible that the extensity of IVPD decreases with higher spatial resolution and higher wave speed (or stiffness) and increases with the amplitude of the vibration. These simulations are in line with our experimental observations illustrated in figure 3. We performed the numerical IVPD inversion for the experimental situation that yielded the highest IVPD effect (matrix size 32x32 and high amplification of the mechanical vibration). The inversion result is shown in figure 4. The spatially averaged stiffness values ± standard error are in the inner (outer) region 1.75 (6.53) ± 0.25 (0.54) kPa.Discussion
In the presented experiments the extent of IVPD increased with increasing voxel size and vibration amplitude. Our observations are in line with the simulations and the numerical inversion results prove that voxel stiffness can be assessed by fitting eq. 1 to vibration induced signal loss without using spatial differences. However, we were able to observe a significant IVPD effect only in the softer inner part of the phantom.Conclusion
IVPD-MRE may provide a higher effective spatial resolution of stiffness maps than phase-contrast based MRI. The technique has the potential to detect pathologies with dimensions close to the voxel size, but requires a careful adjustment of the experimental parameters to the expected stiffness rangeAcknowledgements
No acknowledgement found.References
1. Venkatesh S, Ehman R. Magnetic Resonance Elastography, Springer, New York, 2014.
2. Manduca A, Oliphant T, Dresner M et al. Magnetic resonance elastography: Non-invasive mapping of tissue elasticity. Med Image Anal. 2001; 5: 237–254.
3. Glaser K, Felmlee J, Manduca A, et al. Shear stiffness estimation using intravoxel phase dispersion in magnetic resonance elastography. Magn Reson Med. 2003; 50(6):1256-1265.
4. Yin Z, Kearney S, Magin R, et al. Concurrent 3D acquisition of diffusion tensor imaging and magnetic resonance elastography displacement data (DTI-MRE): Theory and in vivo application. Magn Reson Med. 2016; DOI:10.1002/mrm.26121 (in print).
Figures