1372

Anisotropic shear modulus estimation in ex vivo white matter of the brain using magnetic resonance elastography and finite element modeling
John L Schmidt1, Dennis J Tweten1, Ruth J Okamoto1, Andrew A Badachhape2, Joel R Garbow3, and Philip V Bayly1,2

1Mechanical Engineering and Materials Science, Washington University in St. Louis, St. Louis, MO, United States, 2Biomedical Engineering, Washington University in St. Louis, St. Louis, MO, United States, 3Radiology, Washington University in St. Louis, St. Louis, MO, United States

Synopsis

White matter in the brain is thought to be mechanically anisotropic and vulnerable to mechanical strain. By studying mechanical shear wave propagation in ex vivo brain tissue using magnetic resonance elastography (MRE), and comparing to results from computer models, shear moduli and shear anisotropy were estimated. This method allows the relaxation of assumptions of isotropy and homogeneity in traditional MRE inversions. The ratio of shear moduli governing shear parallel and perpendicular to fiber direction was approximately 1.25, indicating mild anisotropy in shear. This quantitative characterization of shear anisotropy in white matter has important implications for traumatic brain injury modeling.

Objective

White matter (WM) in the brain exhibits anisotropic mechanical properties,1 which likely play an important role in the mechanics of traumatic brain injury.2 Magnetic resonance elastography (MRE) allows the estimation of mechanical properties in soft tissue from phase-contrast MRI of propagating shear waves. Most MRE analyses assume brain-tissue isotropy and homogeneity. Transversely isotropic (TI), nearly incompressible, viscoelastic models can describe anisotropic tissue with one dominant fiber direction. The simplest anisotropic material model for small deformations in soft tissue is a three-parameter TI model, including shear anisotropy (Φ=μ1/μ2-1), tensile anisotropy (ζ=E1/E2-1), and minimum shear modulus (μ2). While not all WM has a single, dominant fiber direction, TI models are a feasible next step towards understanding its anisotropic behavior.

Methods

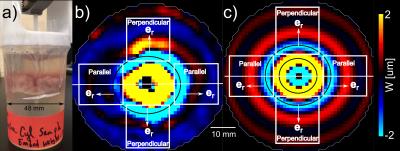
Brains from N=8 female domestic pigs (age 3 months, 40-45 kg) were extracted immediately after euthanasia. A disk shaped sample (~42 mm diameter; ~14 mm thick), consisting of both WM and grey matter, was dissected from the corpus callosum and surrounding areas, and was embedded in gelatin/glycerol3 in a ~48-mm ID container. A 3-mm diameter plastic rod, excited by a piezoelectric actuator (APA150M, Cedrat Technologies) provided central axial (z) excitation at 100, 200, and 300 Hz, generating radially-propagating shear waves (n ≈ eR). Imaging was performed at 4.7 tesla at room temperature with an Agilent/Varian DirectDrive imaging system. Diffusion tensor imaging (DTI) experiments were performed to confirm axonal orientation (30 directions, b=2000 s/mm2). The time from euthanasia to the start of DTI/MRE was ~1-2 hr. Shear-wave fronts exhibited elliptical propagation in slices containing mainly WM, suggesting transverse isotropy.4 A 3D, finite-element (FE) model of the MRE experiment was created using COMSOLTM Multiphysics 5.1. In the FE model, a cylindrical inclusion with TI material properties (representing brain tissue) was embedded in a “gelatin” cylinder (48 mm diameter; 48 mm long; shear storage modulus, μ=1.1 kPa; loss factor, η=0.1; density, ρ=1100 kg/m3). Axial harmonic excitation of 25 μm was provided at 100, 200, and 300 Hz on the inner radius (1.5 mm). The baseline storage modulus of the inclusion, μ2,i was varied from 0.6 - 6 kPa, with loss modulus η=0.5. Shear anisotropy, Φ, was varied from 0 to 1. Tensile anisotropy (nonzero ζ) was not included; ζ does not affect pure transverse ("slow") shear waves induced by excitation normal to fiber direction. To estimate material properties, apparent shear storage modulus (denoted G+) was calculated in both MRE experiments and FE simulations using local direct inversion (LDI).3 MRE and FE inversion results were averaged within regions of interest (ROIs) to highlight fiber orientation effects (see Figs. 1 b,c). FE models with G+ most similar to the MRE experiment were deemed to best describe μ2 and Φ within WM.

Results

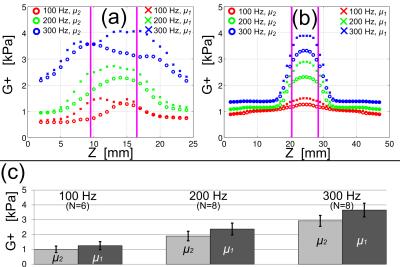
Shear-wave images from MRE (Fig. 1b) and FE models (Fig. 1c) are shown below. In experiments, apparent shear modulus was higher in slices containing WM (slice position 9<z<17, Fig. 2a) in ROIs in which waves propagated parallel to the fiber direction (μ1, Fig. 2a). This indicates higher shear stiffness parallel to the fiber axis, consistent with TI behavior. Elliptical waves observed in experiment exhibited semi-axis ratio a/b = 1.1 ± 0.05 (mean±std). Simulations exhibited similar semi-axis ratios for shear anisotropy values 0.15<Φ<0.40 with Φ = 0.25 corresponding to the mean semi-axis ratio a/b = 1.1. Baseline shear modulus (μ2) and the shear modulus parallel to fibers, μ1, were estimated for N=8 samples at 100, 200, 300 Hz with results shown in Fig. 2c.

Discussion

Shear anisotropy was estimated in the ex vivo porcine brain by comparing FE simulations to MRE experiments. Frequency-dependent shear moduli for shear in planes perpendicular (μ2), and parallel (μ1) to the fiber direction were obtained. Shear-wave fronts were fit to ellipses in both simulation and experiments, leading to estimated shear anisotropy Φ = 0.25 (0.15<Φ<0.40). Limitations of this work include the assumption that the material is linearly viscoelastic with isotropic loss factors typical of brain (0.5) and gelatin (0.1). However, the use of FE modeling, rather than standard inversion algorithms, allows us to relax the usual assumptions of isotropy and local homogeneity. The experimental protocol and FE model used in this study do not elucidate tensile anisotropy, ζ, which would involve fiber stretch induced by “fast” shear waves. The current study provides clear quantitative data showing anisotropy of shear moduli of brain tissue, which enhances our understanding of the mechanical properties of WM in the brain, and provides data for comparison to estimated WM properties in vivo. Future work will focus on robust, automated methods for the intact, living brain.

Acknowledgements

Funding: NIH NS055951, NSF CMMI-1332433

References

1. Feng Y, et al., Measurements of mechanical anisotropy in brain tissue and implications for transversely isotropic material models of white matter. J Mech Behav Biomed. 2013; 23:117-132.

2. Guirdano C, et al., The influence of anisotropy on brain injury prediction. J Biomech. 2014; 47(5):1052-1059.

3. Schmidt JL, et al., Magnetic resonance elastography of slow and fast shear waves illuminates differences in shear and tensile moduli in anisotropic tissue. J Biomech. 2016; 49(7): 1042-1049

4. Okamoto RJ, et al., Viscoelastic properties of soft gels: comparison of magnetic resonance elastography and dynamic shear testing in the shear wave regime. Phys Med Biol. 2011, 56(19):6379-6400.


Figures

Figure 1: (a) MRE experient: Brain tissue embedded in gelatin 1-2 hr post-mortem. (b) Experimental MRE of porcine brain ex vivo. (c) FE simulation (COMSOLTM) of a similar sample (μ2,i = 2.5 kPa; Φ=0.25). Fitted ellipses are drawn in black. The major axis of each ellipse is highlighted by a white line. The indicated regions of interest (ROIs) were used to estimate average shear wavelength for waves propagating parallel and perpendicular to the dominant fiber orientation.

Figure 2: (a) Average apparent shear storage modulus (G+) from LDI vs z-coordinate of the imaging slice in a single-sample MRE experiment at 100, 200, and 300 Hz actuation. (b) Average apparent shear storage modulus (G+) from LDI vs z-coordinate of the imaging slice in an analogous FE simulation (100 Hz: μ2,i = 1.2 kPa, Φ=0.25; 200 Hz: μ2,i = 2.2 kPa, Φ=0.25; 300 Hz: μ2,i = 3.0 kPa, Φ=0.25). (c) Average shear storage moduli from FE models that provide best matches to experiments for N=6 samples (100 Hz) and N=8 samples (200 and 300 Hz).

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
1372