Synopsis

The increasing use of MR elastography demands that fast, robust, and out-of-the-box reconstruction methods are available. A new local direct method is presented here to fit these needs. The method utilizes the finite element method, assumes that stiffness is locally homogeneous, and includes additional advancements that improve quality and robustness. Efficacy of the proposed method is demonstrated across phantoms and volunteer data in the brain and breast. The method is contrasted with other standard techniques, showing similar or improved accuracy and robustness, improved computational cost and an independence from regularization parameters.

Purpose

Introduction

As MR elastography becomes more widely used clinically, it is imperative that fast and dependable out-of-the-box reconstruction methods are available. MRE demands methods that give reliable and accurate maps of stiffness, but invariably these algorithms must cope with practicalities such as noise, artifacts, and wave behavior that may locally veer from material assumptions. These factors may pollute methods that reconstruct data globally; however, local methods typically suffer due to the assumption of local stiffness homogeneity.

A local direct method is presented here with a number of computational advancements that improve the resulting stiffness distributions, address noise, and reduce computational time. It will be shown that the proposed method can recover nearly the same degree of detail in phantoms as slower global methods that account for stiffness heterogeneity while providing robust reconstructions of complex anatomical data.

Methods

The proposed reconstruction method uses finite element (FE) analysis and assumes stiffness is locally homogeneous; however, unlike some similar methods does not assume local pressure homogeneity. It considers time-harmonic data and assumes tissue is an isotropic incompressible linear elastic material. Like other local methods, it traverses an image stack of MRE displacement data, performing a small reconstruction centered at each voxel.

Several approaches to minimize the effects of noise are utilized. These include pre-computing displacement derivatives by polynomial fitting and using a unique finite element which is inf-sup stable ¹ but linear in both displacements and pressure. Additional advancements improve the resulting elastogram and reduce computational time. The size of the local FE mesh is reduced by using tetrahedral elements, which increases the validity of the local homogeneous assumption and decreases the size of the system to solve thereby lowering computational time. The test functions in the FE analysis are chosen to be divergence free so that the pressure term is removed which further reduces the system size. Invalid equations are removed and weighted averaging is applied which increase the accuracy and robustness of the resulting elastogram.

The proposed local method is compared to two other methods. The first is a difference-based local method which uses the curl operator to remove the compressional component from the wave data.² The second is a global method which accounts for stiffness heterogeneity and also uses FE analysis.^3,4

Results and Discussion

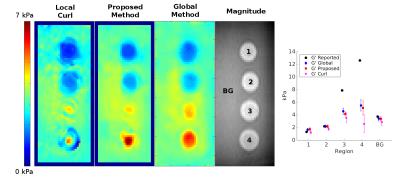
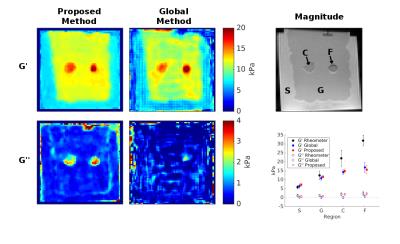
The three methods are applied to data from the CIRS 049 elastography phantom with results shown in Figure 1. The proposed method is shown to more accurately estimate the storage modulus, G’, and provide better resolution of inclusion boundaries than the curl method. The proposed method exhibits comparable accuracy to the global method but requires an order of magnitude less compute time (7 and 73 seconds, respectively). The global method additionally requires tuning of regularization parameters to the dataset in order to construct optimal results. Both G’ and G’’ results from the proposed and global methods applied to a breast phantom are shown in Figure 2. The proposed method approaches the accuracy of the global method for G’ but gives a better resolved and more plausible solution for G’’.

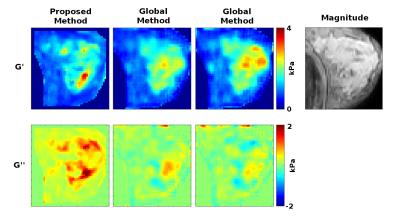
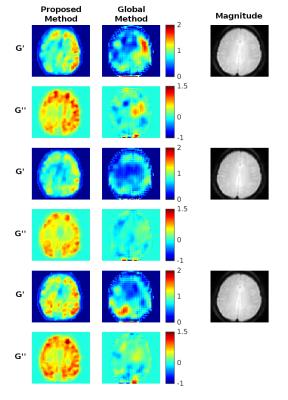
The proposed and global methods are also applied to volunteer breast and brain data, with results shown in Figures 3 and 4. Both methods show agreement with anatomy in breast although the global method gives negative values for G’’ and shows ambiguity in stiffness between different choices of regularization parameters. For the brain data, the proposed method gives consistent reconstructions between the three datasets for both G’ and G’’. The parameters for the global method were chosen based on G’ for the second dataset which showed symmetry and correspondence to anatomy. However, the remaining G’ and G’’ results do not seem to match anatomy or display symmetry. This may indicate a requirement to tune the parameters by dataset even within the same case.

Conclusion

Acknowledgements

References

1. Quarteroni A, Valli A. Numerical Approximation of Partial Differential Equations. 1994; Springer.

2. Sinkus R, Tanter M, Xydeas T, Catheline S, Bercoff J, Fink M. Viscoelastic shear properties of in vivo breast lesions measured by MR elastography. Magn. Reson. Imaging. 2005; 23(2,SI):159-165.

3. Park E, Maniatty A. Shear modulus reconstruction in dynamic elastography: time harmonic case. Phys. Med. Biol. 2006; 51:3697-3721.

4. Honarvar M, Sahebjavaher R, Salcudean S, Rohling R. Sparsity regularization in dynamic elastography. Phys. Med. Biol. 2012; 57:5909-5927.