1357

Toward an Optimized Dictionary for Pattern Matching in Magnetic Resonance Fingerprinting
Kun Yang1, Yun Jiang1,2, Mark Griswold1,2, Vikas Gulani1,2, and Debra McGivney2

1Dept. of Biomedical Engineering, Case Western Reserve University, Cleveland, OH, United States, 2Dept. of Radiology, University Hospitals of Cleveland, Cleveland, OH, United States

Synopsis

An important issue in magnetic resonance fingerprinting (MRF) is the precision of pattern matching. The sensitivity of inner product between the signal and dictionary can be corrupted by closely spaced dictionary entries. In order to make MRF more sensitive and precise, four modifications of the MRF dictionary are proposed. The performance of each method is tested and compared over 30 repetitions in a phantom scan. Some of the methods demonstrate a significant reduction in the error over the original MRF dictionary.

Purpose

Magnetic resonance fingerprinting 1 (MRF) is a novel technique which allows for the quantification of different MR parameters simultaneously using one acquisition. The measurement from a voxel signal is matched to a pre-calculated dictionary using pattern matching. However, one issue in MRF is the separation of closely spaced dictionary entries, which is related to the precision of the method. In order to make the MRF more sensitive and precise, we propose several methods to expand the dictionary to achieve better matching performance.

Method

The matching process may have a higher sensitivity when the curvature of the inner product is increased around the correct match. 2 We look to achieve this by expanding the dictionary to take advantage of multiple time points in the matching. Denoting the original MRF dictionary by D, we create a new matrix A, which is derived by applying linear combinations of D across the time domain, and combine A with D to form a larger dictionary . To perform pattern matching with the modified dictionaries, the same transformations are applied to the reconstructed voxel signals also.

Four methods were considered to create a modified dictionary.

1. Neighbor subtraction: A finite difference approximation of the dictionary is computed, in which adjacent points are subtracted to form the matrix A.

2. Whole Block subtraction. The signal evolution tends to exhibit block like structure related to the flip angle pattern used in the acquisition. Adjacent subtraction between blocks are applied in this method: subtract block 1 from block 2, subtract block 2 from block 3, etc. An example is shown in Figure 2.

3. Half block subtraction. Noting the symmetry within blocks from the previous method, here we use these blocks to subtract the left half from the right within each block across the time course for each entry.

4. One Two block subtraction. Our initial tests suggest that method 2 achieves better results, therefore, as an extension, we tried different block subtraction combinations. Method 2 is used method as matrix A', and following the same idea, use two block subtraction as matrix A'', both A' and A'' are added along with D to form.

For evaluation of these approaches, A FISP-based MRF acquisition 3 was used to scan two slices using the ISMRM/NIST MRI system phantom, 4 one through each of the T1 and T2 arrays, with an in-plane spatial resolution of 1.2 × 1.2 mm2 and a slice thickness of 5 mm. 3000 frames were acquired for each slice. The dictionary D was created using Bloch simulations (T1 range, denoted as min:step:max is: 10:10:100, 120:20:1000, 1040:40:2000, 2050:100:3000ms; T2 range is 2:2:10, 15:5:100, 110:10:300, 350:50:800 ms). The percent error over each tube was computed using the true phantom values from gold standard spin echo methods for reference.

Results

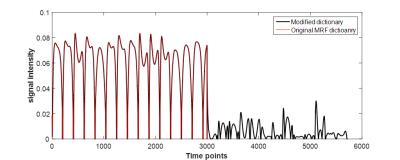
To demonstrate the increase in curvature seen around the correct match, we selected one dictionary entry from both D and (T1 = 940 ms, T2 = 40 ms) and computed the inner product between these entries with their respective dictionaries. The absolute value of this test is shown in Figure 1, with the correct match indicated by a dashed line. The original result using D is shown in red, the result using the modified dictionary is in blue.

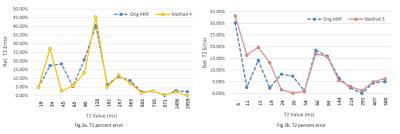
The percent error for each of the methods is calculated over each tube. We show the best performing methods for T1 and T2 separately in Figure 3. The T1 matching of method 4 is demonstrated as a green line in Figure 3a. The yellow line in Figure 3b is the T2 matching of method 3. Each of the respective methods performs better than the original MRF dictionary in a majority of the tubes in the phantom.

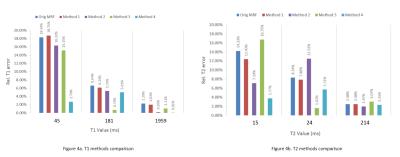
Figure 4 demonstrates the performance between these four methods using three tubes as examples. Notice that some methods demonstrate a significant reduction in the error over the original MRF dictionary, however, the performance of the different methods varies.

Discussion and Conclusion

Four modifications of the MRF dictionary are proposed and developed in this work. While error reduction is not seen for all T1, T2 values in the phantom, we believe that extensions of these methods will achieve more consistent and improved results. We note that while we have increased the size of the dictionary , compression methods 5 and fast matching algorithms 6 are available if the dimensionality becomes too large. Finally, despite the modifications made to the dictionary, the MRF acquisition remains unchanged, and does not require additional scan time.

Acknowledgements

The authors would like to acknowledge funding from Siemens Healthcare and NIH grants 1R01EB016728-01A1 and 5R01EB017219-02.

References

1. Ma D, et al. Magnetic Resonance Fingerprinting. Nature. 2013; 495:187-192.

2. Amthor T, Doneva M, Koken P, Keupp J, and Bornert P, “Comparison of different approaches of pattern matching for MR fingerprinting,” in Proceedings of the 23rd Annual Meeting, ISMRM, 2015, p. 3394.

3. Jiang Y, Ma D, Seiberlich N, Gulani V, Griswold MA. MR fingerprinting using fast imaging with steady state precession (FISP) with spiral readout. Magn. Reson. Med. 2015; 74:1621–31.

4. Russek SE, Boss M, Jackson EF, Jennings DJ, Evelhoch JL, Gunter JL, Sorensen AG, “Characterization of NIST/ISMRM MRI system phantom,” in Proceedings of the 20th Annual Meeting, ISMRM, 2012, p. 2456.

5. D. McGivney, E. Pierre, D. Ma, Y. Jiang, H. Saybasili, V. Gulani, and M. Griswold, “SVD compression for magnetic resonance fingerprinting in the time domain,” IEEE Trans. Med. Imaging, vol. 0062, pp 1-13, 2014.

6. S. F. Cauley, K. Setsompop, D. Ma, Y. Jiang, H. Ye, E. Adalsteinsson, M. Griswold, and L. Wald, “Fast group matching for MR fingerprinting reconstruction,” Magn. Reson. Med., vol 528, pp 523-528, 2014.

Figures

Figure 1. Absolute value of the inner product of the dictionary with a given signal (T1 = 940 ms, T2 = 40 ms). The original MRF dictionary D is plotted in red, while the block wise subtraction dictionary (method 2) is in blue. The correct match is indicated by the dashed line. Note the increase in curvature around the correct match for the blue curve, indicating a more sensitive matching scheme.

Figure 2. Signal evolution of the original MRF-FISP dictionary (T1=940 ms, T2=40 ms) is marked as a red line. Black line is the signal evolution of the modified dictionary (Method 2 whole block subtraction). The first 3000 time points are the same, the modified dictionary signal is extended to increase sensitivity.

Figure 3. Figure 3a shows that method 4 outperforms MRF in 9 out of 14 tubes for T1 matching, with highest error reduction of 15.6% at T1 = 45 ms. Method 3 outperforms MRF in 5 out of 14 tubes for T2 matching. For T2 greater than 24, we see either improvement or very similar results, however, for T2 values smaller than 24, Method 3 increases the errors.

Figure 4. The relative error for these four methods using three tubes as examples. In T1=1959 ms, methods 2 and 4 are very close to the true value, and most regions in has better performance. Examples for T2 are shown in (b). While reduced error is seen in some of the tubes and for some of the methods, a consistent method is not seen.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
1357