Synopsis

We present work to optimize the parameters used in the Bayesian approach to partial volume in MRF. Care needs to be taken when choosing parameter values to balance effects from noise and over regularization of the solution. MRF brain data from a normal volunteer is analyzed to determine the optimal parameters in separating white matter from gray matter and gray matter from CSF. Parameter choices are confirmed by examining the results from our algorithm in regions of pure white matter.

Purpose

Methods

Using the Bayesian statistical framework, no assumptions are made as to how many or which tissue types are present in any given voxel. Consider a voxel signal y as a weighted sum of the MRF dictionary D, plus Gaussian noise e,

$$ y = Dx + e.$$

Assume that the weight vector x is sparse, meaning only a few tissue types have significant contribution to the signal. We model x as a zero mean Gaussian random variable with unknown variance θ. To encourage sparsity, θ is modeled as a Gamma random variable with shape and scale parameters α and β, respectively. Applying Bayes’ formula yields

$$ \arg \min_{x,\theta} \left\{ \frac{1}{2} \| y - D x \|_2^2 + \frac{1}{2} \mu^2 \| T^{-1/2}_\theta x \|_2^2 + \frac{1}{\beta}\sum_{j = 1}^n \theta_j + \left( \alpha - \frac{3}{2} \right) \sum_{j = 1}^n \log \theta_j \right\} $$

which is solved iteratively in an alternating fashion. ² The matrix T_θ is diagonal, corresponding to the variance of each weight x_j. There are three parameters to be tuned: the Gamma parameters α and β, and regularization parameter μ.

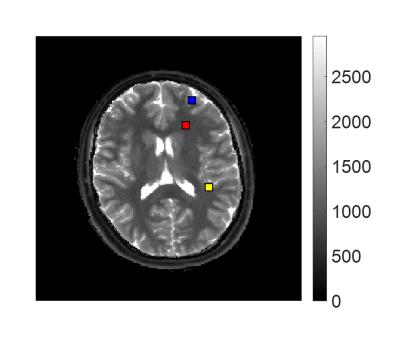
We applied this algorithm to the results from a normal volunteer previously scanned in an IRB approved study using an MRF-FISP acquisition. ⁴ Voxels were chosen in regions where we expect to see partial volume: white matter/gray matter (WM/GM) and GM/CSF, as well as one voxel within pure WM.

The dictionary D contained 5970 simulated signals, each with 3000 time points, corresponding to one combination of T₁ and T₂. To improve the results and computational efficiency, the dictionary was trimmed at each iteration, removing entries which correspond to the smallest 5% of the weights. 110 iterations were run, resulting in 21 triplets of T₁, T₂, and tissue weight, to explain the signal in each voxel. The locations are indicated in the MRF T₁ map in Figure 1.

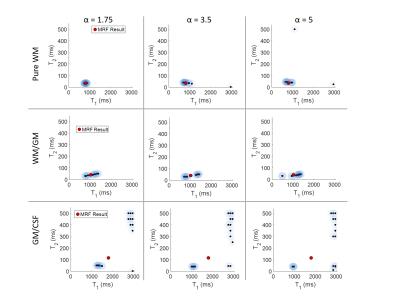
Fixing the regularization parameters (μ=0.001), we tested different combinations of Gamma parameters. When varying α, we set β=0.1, and when varying β, α was fixed at 1.75.

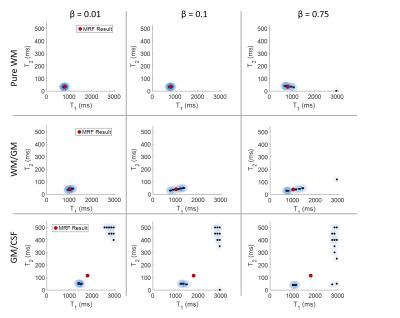
With a fixed Gamma distribution (α=1.75, β=0.1), we tested a range of regularization parameters in a logarithmic scale from 0 to 1.

Visualization is a challenge. Each voxel presents a multidimensional result of T_1, T₂ pairs with their corresponding weights. Results are presented on a voxel-wise basis using T₁, T₂ scatter plots, with the weight overlaid on top of each point using a proportional color intensity.

Results

Results are shown in Figures 2-4. We use the pure white matter voxel as a guide for examining the parameters. When α=3.5 and 5, the results for white matter are spread out and show erroneous T₁, T₂ pairs, whereas when α=1.75, a tight cluster around the MRF result is seen, which is expected from this pure region. Similar results are seen in white matter for varying β.

For separating white and gray matter, α=3.5 does the best job, showing two distinct clusters, however, across tissue boundaries, not much variation is seen when changing α and β.

In the case of the regularization parameter, when μ=0, all three voxels show the result of a least squares fitting. As μ is increased, the results begin to converge; in the case of pure white matter, when μ=0.01, a tight cluster forms around the MRF values, with no erroneous pairs. In the case of the PV-affected voxels, several dominant clusters are shown at μ=0.001, 0.01. For WM/GM, the results begin to converge toward the MRF result as μ is increased beyond 0.01. For GM/CSF, the results do not converge until μ=1.

Discussion and Conclusion

We have presented an analysis of the parameters within the Bayesian MRF PV framework. The parameters which did not vary were fixed based on previous experience with an MRF-FISP dataset as well as by observing the performance of the algorithm in pure white matter. Our results here show some consistency within the Gamma parameters, and the highest sensitivity to the regularization parameter. As μ increases, our results converge toward the effective MRF results. This parameter may also be sensitive to the types of tissues we are trying to separate; white matter and gray matter have much closer T₁, T₂ values than do gray matter and CSF.

Further tuning of these parameters should improve the results, in particular in voxels where partial volume is present.

Acknowledgements

References

1. Ma D, et al. Magnetic resonance fingerprinting. Nature. 2013; 495:187-192.

2. McGivney D, et al. The partial volume problem in MR fingerprinting from a Bayesian perspective. Proceedings of the 24th Annual Meeting, ISMRM. 2016, p 435.

3. Calvetti D & Somersalo E. Hypermodels in the Bayesian imaging framework. Inverse Problems. 2008; 24:034013.

4. Jiang Y, et al. MR fingerprinting using fast imaging with steady state precession (FISP) with spiral readout. Magn. Reson. Med. 2015; 74:1621-1631.