1353
Fast Analytical Solution for Extreme Unaliasing of MR Fingerprinting Image Series1Imaging Division, The Florey Institute of Neuroscience and Mental Health, Melbourne, Australia, 2Biomedical Engineering, Case Western Reserve University, Cleveland, OH, United States, 3Radiology, Case Western Reserve University & University Hospitals, Cleveland, OH, United States
Synopsis
A non-iterative analytical solution to the MRF image reconstruction problem is presented. The method performs a direct interpolation of the acquired k-space points based on a singular-vector basis of fingerprints from a first-pass MRF estimate. The method is shown to drastically reduce spatio-temporal aliasing, allowing accurate T1 and T2 measurements for a single slice with a 7.6s acquisition, without need for auto-calibration data, and with computational overhead an order of magnitude faster than previously reported iterative image-based methods.
Introduction
Reducing aliasing artefacts in MR Fingerprinting(1) (MRF) image series can drastically improve parameter mapping accuracy(2–5). Most aliasing-reduction methods work in the x-t domain, requiring several gridding/de-gridding iterations, often with empirically chosen parameters to control convergence(2–4). Additionally, each voxel is forced to match a single tissue type, potentially biasing multi-component fingerprint analysis(6,7). An iterative k-t domain approach has also been proposed, dispensing of gridding/de-gridding steps, but requiring the acquisition of an auto-calibration dataset(5).
Here we present a novel k-space approach to directly reconstruct a fully sampled data series after a single pre-processing step, with no requirement for auto-calibration sets. The method enables accurate T1 and T2 mapping for a single slice within a 7.6s acquisition, with computational overhead an order of magnitude smaller than previously reported x-t methods.
Theory
Let $$$X$$$ be the target image-series to reconstruct, and $$$Y$$$ the undersampled acquired data. For a k-space location k visited at timepoint t, we have
$$Y(k,t)=G_{k}X(t) \color{white}{-----------}[1] $$
with $$$G_{k}$$$ the k-space encoding matrix for $$$k$$$. The method aims to retrieve $$$Y(k,t)$$$ for all $$$t$$$, referred as $$$Y_{r}$$$.
First, instead of acquiring a low-resolution autocalibration data set, the method performs an initial MRF analysis(1) on a zero-filled $$$Y$$$ to find a basis set as follows:
All fingerprints selected during the matching process are gathered in a matrix $$$\hat{X}$$$, an estimate of $$$X$$$. $$$\hat{X }$$$ should be compressible to a small basis of singular vectors $$$U_{\hat{X}}$$$(8), with $$$U_{\hat{X}}$$$ able to approximate any linear combination of fingerprints in $$$\hat{X }$$$. But $$$U_{\hat{X}}$$$ should also approximate fingerprint combinations in $$$X$$$, such as $$$Y(k)$$$ in [1]. We can then retrieve $$$Y_{r}$$$ by interpolating between acquired points of $$$Y$$$ with $$$U_{\hat{X}}$$$. The following algorithm is used to ensure proper conditioning of the interpolation problem:
$$$\color{white}{----}\circ$$$Perform standard MRF analysis to compute $$$\hat{X}$$$:
$$$\color{white}{----}\circ$$$For each $$$k$$$:
$$$\color{white}{--------}$$$1. Perform SVD analysis on $$$S_{k}\hat{X}=U_{\hat{X},k} Σ_{\hat{X},k}V_{\hat{X },k}^{H}$$$ , with $$$S_{k}$$$ the temporal decimation operator selecting the acquired time points for $$$k$$$.
$$$\color{white}{--------}$$$2. Discard any singular vector of $$$U_{\hat{X },k}$$$ whose singular value is less than 1% of the highest one.
$$$\color{white}{--------}$$$3. Set $$$W_{k}=U_{\hat{X },k}^{H}S_{k}Y(k)$$$
$$$\color{white}{--------}$$$4. Set $$$U_{\hat{X}}=\hat{X}V_{\hat{X},k}(Σ_{\hat{X},k})^{-1}$$$
$$$\color{white}{--------}$$$5. Set $$$Y_r (k,t)=\begin{cases}Y(k,t) & if\space k\space sampled\space at\space t \\U_{\hat{X}}(k,t)W_{k} & otherwise\end{cases}$$$
$$$\color{white}{----}\circ$$$Perform inverse non-uniform-FFT (nuFFT) on $$$Y_{r}$$$ and perform MRF analysis.
To speed up the reconstruction, temporal compression was applied before each nuFFTs and MRF analysis(9). Due to the use of SVD in both k-space and time, the proposed method is referred to as kt-SVD-MRF.
Methods
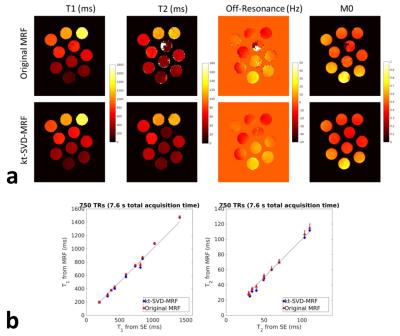
The method was tested for an MRF acquisition as reported in (1). Reconstruction was performed using single-threaded Matlab(10) on a computation server (128 Gb of RAM). The method’s accuracy was tested on an agar phantom consisting of 10 vials of different T1 and T2 values, imaged with the above sequence at 3T on a Skyra scanner (Siemens, Erlangen, Germany) over 3000 TRs (256x256 matrix size, 300mm FOV). T1 and T2 values were measured with a Spin-Echo sequence for comparison. Standard MRF analysis and kt-SVD-MRF were applied on the full-length image series for reference, then truncated to the first 750 TRs. Image series were compressed in the time-domain whenever applicable onto 300 eigen-timepoints. The T1 and T2 values were then measured over an ROI within each vial.The same MRF sequence was also used on an invivo dataset of a healthy volunteer in compliance with an ethics committee.Results and Discussion
The computational overhead (Figure 1) compared to conventional MRF is slightly more than a factor 2, compared to a factor 25 reported in previously reported x-t methods(3,4). Most of the numerical effort was from the gridding and SVD interpolation steps, which are easily parallelizable.
The results of the agar phantom experiment are displayed in Figure 2. Both methods were in good agreement with Spin-Echo-based measurements (concordance-correlation coefficients >0.99 for all parameters). As the signal within each ROI was more uniform with kt-SVD-MRF, the mean T1 and T2 values appeared closer to a specific dictionary fingerprint, but with reduced error standard-deviation.
For invivo experiments with 750 TRs (Figure 3), standard MRF maps present obvious errors over the ventricle and cutaneous areas. In comparison maps from kt-SVD-MRF were in good agreement with their 3000-TR reference. Representative frames and temporal signal obtained with kt-SVD-MRF are displayed in Figure 4. Image series show drastically reduced spatial (4a) and temporal (4b) aliasing.
Therefore kt-SVD-MRF could allow accurate T1 and T2 mapping within 7.6s acquisition for a single slice at 1.2mm isotropic resolution, using a signal interpolation close to the ground truth signal, without need for computationally intensive iterations, convergence parameters or autocalibration-set and compatible with multi-compartment parameter analysis.
Acknowledgements
No acknowledgement found.References
1. Ma D, Gulani V, Seiberlich N, Liu K, Sunshine JL, Duerk JL, Griswold M a. Magnetic resonance fingerprinting. Nature 2013;495:187–92.
2. Davies M, Puy G, Vandergheynst P, Wiaux Y. A Compressed Sensing Framework for Magnetic Resonance Fingerprinting. SIAM J. Imaging Sci. 2014;7:27.
3. Pierre EY, Ma D, Chen Y, Badve C, Griswold MA. Multiscale reconstruction for MR fingerprinting. Magn. Reson. Med. 2016;75:2481–2492.
4. Cline CC, Chen X, Mailhe B, Wang Q, Nadar M. AIR-MRF: Accelerated iterative reconstruction for magnetic resonance fingerprinting. In: Proceedings of the 24th Annual Meeting of ISMRM. Singapore; 2016. p. 434.
5. Doneva M, Amthor T, Koken P, Sommer K, Börnert P. Low Rank Matrix Completion-based Reconstruction for Undersampled Magnetic Resonance Fingerprinting Data. In: Proceedings of the 24th Annual Meeting of ISMRM. Singapore; 2016. p. 432.
6. Deshmane A, Ma D, Jiiang Y, Fischer E, Seiberlich N, Gulani V, Griswold MA. Validation of Tissue Characterization in Mixed Voxels Using MR Fingerprinting. In: Proceedings of the 22nd Annual Meeting of ISMRM. ; 2014. p. 94.
7. McGivney D, Deshmane A, Jiang Y, Ma D, Griswold MA. The Partial Volume Problem in MR Fingerprinting from a Bayesian Perspective. In: Proceedings of the 24h Annual Meeting of ISMRM. Singapore; 2016. p. 435.
8. Cauley SF, Setsompop K, Ma D, Jiang Y, Ye H, Adalsteinsson E, Griswold MA, Wald LL. Fast group matching for MR fingerprinting reconstruction. Magn. Reson. Med. 2014;528:523–528.
9. McGivney D, Pierre E, Ma D, Jian Y, Saybasili H, Griswold MA. SVD Compression for Magnetic Resonance Fingerprinting in the Time Domain. IEEE Trans. on Med. Imaging 2014;33:12
10. The Mathworks, Natick, MA
Figures
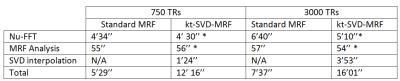
Computation times. *Average time between the 2 operations