Synopsis

Fusing a lower resolution color image with a higher resolution monochrome image is a common practice in medical imaging. By incorporating spatial context and/or improving the Signal-to-Noise ratio, the fused image provides clinicians with a single frame of the most complete diagnostic information. In this paper, image fusion is formulated as a convex optimization problem which avoids image decomposition and permits operations at the pixel level. This results in a highly efficient and embarrassingly parallelizable algorithm based on widely available robust and simple numerical methods that realizes the fused image as the global minimizer of the convex optimization problem.

Purpose

Theory

Let $$$X=(R,G,B)$$$ denote the color image, and $$$Y$$$ the monochrome image, with $$$R,G,B,Y\in\mathbb{R}^{M\times N}$$$ corresponding to the red, green, blue, and monochrome channels respectively. All values in $$$X$$$ and $$$Y$$$ are in $$$[0,1]$$$. The fused image $$$F=(F_R,F_G,F_B)$$$ results from solving the following problem:

\begin{align} \text{minimize} & \hspace{8pt} \|X-F\|_F^2 + \gamma \, \|f(F_R,F_G,F_B)-Y\|_F^2 \\ \text{subject to} & \hspace{8pt} 0 \leq F \leq 1, \end{align}

where $$$\|\cdot\|_F$$$ denotes the Frobenius norm and $$$f(F_R,F_G,F_B)=w_R\,F_R + w_G\,F_G + w_B\,F_B$$$ is a weighted average of the three color channels; $$$\gamma$$$ is a parameter set by the user. Note that this problem is completely separable across pixels. The result of each pixel is independent of any other pixel. The value of the $$$(i,j)^{\text{th}}$$$ pixel in the fused image can be found by solving the following problem:

\begin{align}\text{minimize} & \hspace{8pt} \left\| \underbrace{ \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ w_R \sqrt{\gamma} & w_G \sqrt{\gamma} & w_B \sqrt{\gamma} \end{bmatrix} }_{\boldsymbol{A}} \, \underbrace{ \begin{bmatrix} \left(F_R\right)_{ij} \\ \left(F_G\right)_{ij} \\ \left(F_B\right)_{ij} \end{bmatrix} }_{\boldsymbol{x}_{ij}} - \underbrace{ \begin{bmatrix} R_{ij} \\ G_{ij} \\ B_{ij} \\ Y_{ij} \sqrt{\gamma} \end{bmatrix} }_{\boldsymbol{b}_{ij}} \right\|_2^2 \\ \text{subject to} & \hspace{8pt} 0 \leq F \leq 1 \end{align}

The solution to this problem can be found by minimizing $$$\|\boldsymbol{A}\,\boldsymbol{x}_{ij}-\boldsymbol{b}_{ij}\|_2$$$ and then performing a projection of the result onto the cube $$$[0,1]^3$$$ along the line $$$l$$$ parameterized by $$$\lambda$$$ in the following equation:

\begin{equation*}l(\lambda) = \left\{ \begin{array}{cl} (R_{ij},G_{ij},B_{ij}) + \lambda\,w & \hspace{4pt} \text{if} \; F_{ij} > 1 \\ (R_{ij},G_{ij},B_{ij}) - \lambda\,w & \hspace{4pt} \text{otherwise} \end{array} \right..\end{equation*}An approximate more computationally efficient solution is to perform a Euclidean projection onto $$$[0,1]^3$$$ (instead of a projection along $$$l$$$). All results are shown using this approximation.

Results

This section presents results of the CLS fusion algorithm for several different applications and compares them to existing fusion algorithms. The weight vector $$$w=(1/3,1/3,1/3)$$$ so that $$$f(X)$$$ yields the intensity channel of the color image [3].

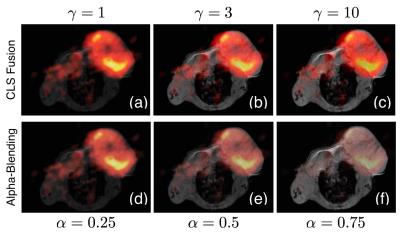
Figure 1 shows results of a 3'-[$$$^{\text{18}}$$$F] fluoro-3'-deoxythymidine PET image and a T1 weighted MR image of a living BALB/c mouse bearing a CT26 colon carcinoma [4]. Increasing $$$\gamma$$$ increases the intensity of the monochrome image in the fused result. These results are compared to alpha-blending [5]. For comparable levels of intensity from the monochrome image, the CLS-fusion algorithm is able to retain much more of the information from the color imagery.

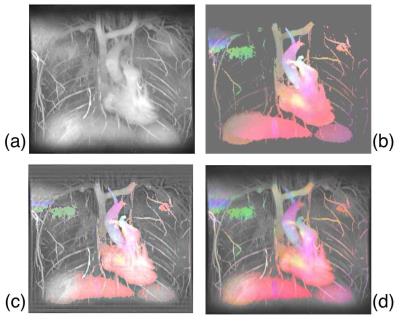
Figure 2 shows MR flow results collected using the Variable-Density Sampling and Radial View-ordering (VDRad) sequence [2]. The velocity in each dimension is represented as a different color; Right-Left (RL) / Anterior-Posterior (AP) / Superior-Inferior (SI) motion are represented by Red/Green/Blue, respectively. Larger velocities are represented with larger color values. Figures 2c and 2d show the result of Wavelet fusion [6] and CLS fusion algorithms, respectively. The Wavelet result shows artifacts resulting from the structure of the Wavelet kernels; these artifacts are absent in the CLS result. Additionally, CLS retains better the color hue better.

Discussion

Acknowledgements

References

[1 ] Gerald Antoch and Andreas Bockisch. Combined PET/MRI: A New Dimension in Whole-body OncologyImaging? European Journal of Nuclear Medicine and Molecular Imaging, 36(1):113–120, 2009.

[2] Joseph Y Cheng, Kate Hanneman, Tao Zhang, Marcus T Alley, Peng Lai, Jonathan I Tamir, Martin Uecker, John M Pauly, Michael Lustig, and Shreyas S Vasanawala. Comprehensive Motion-compensated Highly Accelerated 4D flow MRI with Ferumoxytol Enhancement for Pediatric Congenital Heart Disease. Journal of Magnetic Resonance Imaging, 43(6):1355–1368, 2015.

[3] Jorge Nunez, Xavier Otazu, Octavi Fors, Albert Prades, Vicenc Pala, and Roman Arbiol. Multiresolution-based Image Fusion with Additive Wavelet Decomposition. IEEE Transactions on Geoscience and Remote Sensing, 37(3):1204–1211, 1999.

[4] Martin S Judenhofer, Hans F Wehrl, Danny F Newport, Ciprian Catana, Stefan B Siegel, Markus Becker,Axel Thielscher, Manfred Kneilling, Matthias P Lichy, Martin Eichner, et al. Simultaneous PET-MRI: a New Approach for Functional and Morphological Imaging.Nature Medicine, 14(4):459–465, 2008.

[5] Thomas Porter and Tom Duff. Compositing Digital Images. In ACM Siggraph Computer Graphics,volume 18, pages 253–259. ACM, 1984.

[6] Krista Amolins, Yun Zhang, and Peter Dare. Wavelet Based Image Fusion Techniques — An Introduction,Review and Comparison.ISPRS Journal of Photogrammetry and Remote Sensing, 62(4):249–263, 2007.