1345
T1 and T2 mapping using highly accelerated radial data acquisition and alternating direction method of multipliers1Electrical and Computer Engineering, University of Arizona, Tucson, AZ, United States, 2Department of Medical Imaging, University of Arizona, Tucson, AZ, United States, 3Biomedical Engineering, University of Arizona, Tucson, AZ, United States
Synopsis
Quantitative MRI requires accurate parameter estimation but long acquisition time limits the use of conventional techniques in the clinic. Recently, several T1 and T2 mapping methods based on highly accelerated radial trajectories have been proposed. The reconstruction problems in these works are formulated as unconstrained optimizations and solved using the non-linear conjugate gradient method. We propose an alternative formulation based on the alternating direction method of multipliers which reduces reconstruction time without compromising reconstruction quality.
Introduction
Quantitative characterization of tissues using MR parameter mapping is an important tool in quantitative MRI. Since conventional parameter mapping methods require data acquisition along the temporal (parameter) dimension, they require long acquisition time which limits their practical utility in the clinic. Recently, several T1 and T2 mapping methods based on highly accelerated radial trajectories have been proposed for rapid parameter mapping [1-4]. These methods utilize signal models which allow sparse representations of the signal along the temporal direction together with spatial sparsity constraints. The reconstruction problems in [2-4] are formulated as unconstrained optimization problems and solved using the non-linear conjugate gradient (NLCG) method.Purpose
We propose an alternative formulation based on the alternating direction method of multipliers (ADMM) which offers several advantages including significantly reduced reconstruction time, improved accuracy, and reduced sensitivity to regularization parameter selection.Theory
MR parameter mapping problems in [2-4] can be represented by the unconstrained formulation in Figure 1(a) where $$$E$$$ represents the encoding matrix including the temporal subspace constraints obtained via truncated principal component (PC) decomposition, $$$m$$$ represents the PC images, $$$k$$$ represents the acquired kspace measurements, and $$$\lambda$$$ is the regularization parameter. This problem is solved [2-4] using an NLCG method which has several shortcomings: TV regularization is not differentiable and requires an approximation to obtain the gradient; NLCG is sensitive to the selection of $$$\lambda$$$; Backtracking line search in NLCG is very time-consuming. To address these problems, we propose the constrained formulation in Figure 1(b). The first advantage of this formulation is that regularization parameter $$$\epsilon$$$ can be estimated accurately [5] using the equation in Figure 1(c). This unconstrained formulation can be transformed to a constrained formulation by introducing a feasibility set $$$S$$$ (Figure 1(d)) and decomposed into several sub-problems using ADMM (Figure 1(e)). In Figure 1(e), sub-problem (1) is a simple quadratic minimization problem solved using steepest decent. Sub-problem (2) is solved using a fast and exact algorithm by Chambolle [6]. Sub-problem (3) is simply the orthogonal projection of $$$(Em-dv)$$$ on the closed $$$\epsilon$$$-radius ball centered at $$$k$$$.
Methods
Reconstruction experiments using digital phantoms and in vivo datasets were conducted to compare the performances of the proposed ADMM and NLCG methods [2-4] which were implemented in Matlab. For T2 mapping experiments using the digital phantom, undersampled (R=25) data acquisition using a radial turbo spin-echo (TSE) sequence was simulated matching the data acquisition parameters of a typical in vivo brain acquisition (provided below). Similarly, for T1 mapping experiments using the digital phantom, undersampled (R=25) data acquisition using a radial Steady-State Free-Precession (SSFP) sequence [4] was simulated with typical in vivo brain acquisition parameters. Complex Gaussian noise was added in kspace matching in vivo acquisition SNR. For in vivo T2 mapping, data were acquired on a Siemens Skyra 3T scanner using a radial TSE sequence with echo spacing=7.22ms, ETL=16, TR=1500ms, and 16 radial views/TE with 256 readout points per view. For in vivo T1 mapping, data were acquired on a Siemens Skyra 3T scanner using a radial SSFP sequence [4] with TR =3.72ms, TE=1.86ms, TI=49ms, FA=20 degrees, and 16 radial views/TI with 256 readout points per view. In addition to the accelerated acquisitions, acquisitions with standard sampling (192 views/TE for T2 and 402 views/TI for T1 mapping) were also performed to obtain reference images. A parameter sweep was performed to find the optimal value for λ for NLCG whereas $$$\epsilon$$$ was computed as discussed earlier for ADMM.Results and Discussion
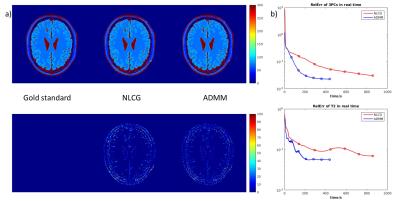
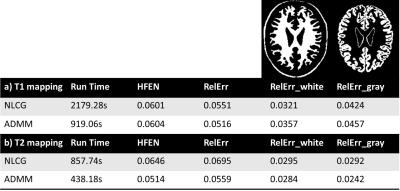
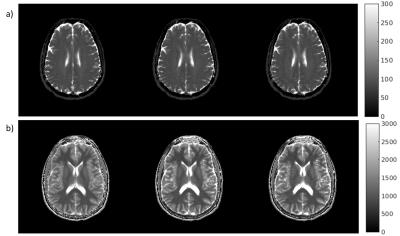
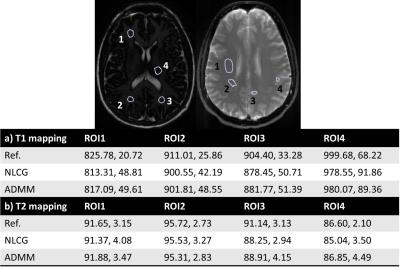
Figures 2 illustrates the results obtained on the digital phantoms for T2. It can be seen that the convergence rate of the proposed ADMM method is substantially faster than that of NLCG. Figure 3 shows several error metrics and reconstruction times calculated during the digital T1 and T2 phantom experiments. These results indicate that ADMM converges faster and provides slightly reduced error at convergence. Figure 4 illustrates the T1 and T2 maps obtained from in vivo data. It can be observed that the visual quality of images from the NLCG and ADMM methods are comparable. To provide a quantitative evaluation in vivo, we also provide a comparison of mean and standard deviation of T1 and T2 values in several ROIs in Figure 5. These results illustrate that both NLCG and ADMM methods yield estimates comparable to the standard sampled reference image.Conclusion
We have proposed a new formulation of MR parameter mapping problem using ADMM. Results from simulations as well as in vivo data have shown that the proposed scheme converges faster without compromising reconstruction quality and has reduced sensitivity to regularization parameter selection.Acknowledgements
Arizona Biomedical Research Commission (ADHS14-082996)References
1. Doneva, Mariya, et al., Compressed sensing reconstruction for magnetic resonance parameter mapping, Magnetic Resonance in Medicine 64.4, (2010):1114–1120.
2. Huang, Chuan, et al. "T2 mapping from highly undersampled data by reconstruction of principal component coefficient maps using compressed sensing." Magnetic Resonance in Medicine 67.5 (2012): 1355-1366.
3. Huang, Chuan, et al. “T2 Relaxometry with Indirect Echo Compensation from Highly Undersampled Data,” Magnetic Resonance in Medicine, 70.4, (2013):1026–1037.
4. Li, Zhitao, et al. “Rapid high-resolution T1 mapping using highly accelerated radial steady-state free-precession acquisition” ISMRM 2016.
5. Afonso, Manya V., et al. "An augmented Lagrangian approach to the constrained optimization formulation of imaging inverse problems." IEEE Transactions on Image Processing 20.3 (2011): 681-695.
6. Chambolle, Antonin. "An algorithm for total variation minimization and applications." Journal of Mathematical imaging and vision 20.1-2 (2004): 89-97.
Figures